Quarter tone

"24 equal temperament" redirects here. For other uses, see Arab tone system.

A quarter tone  play , is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide (aurally, or logarithmically) as a semitone, which is half a whole tone.

Trumpet with 3 normal valves and a quartering on the extension valve (right).

Many composers are known for having written music including quarter tones or the quarter-tone scale (24 equal temperament), first proposed by 19th-century music theorist Mikha'il Mishaqah,[1] and in 1823 by the German theorist Heinrich Richter,[2] including: Pierre Boulez, Julián Carrillo, Mildred Couper, George Enescu, Alberto Ginastera, Gérard Grisey, Alois Hába, Ljubica Marić, Charles Ives, Tristan Murail, Krzysztof Penderecki, Giacinto Scelsi, Ammar El Sherei, Karlheinz Stockhausen, Tui St. George Tucker, Ivan Alexandrovich Wyschnegradsky, and Iannis Xenakis (see List of quarter tone pieces).

Types of quarter tones

Composer Charles Ives chose the four-note chord above as good possibility for a "fundamental" chord in the quarter-tone scale, akin not to the tonic but to the major chord of traditional tonality.[3]  Play  or  play 

The term quarter tone can refer to a number of different intervals, all very close in size. For example, some 17th- and 18th-century theorists used the term to describe the distance between a sharp and enharmonically distinct flat in mean-tone temperaments (e.g., D♯–E♭).[4] In the quarter tone scale, also called 24 tone equal temperament (24-TET), the quarter tone is 50 cents, or a frequency ratio of 21/24 or approximately 1.0293, and divides the octave into 24 equal steps (equal temperament). In this scale the quarter tone is the smallest step. A semitone is thus made of two steps, and three steps make a three-quarter tone  play  or neutral second, half of a minor third.

In just intonation the quarter tone can be represented by the septimal quarter tone, 36:35 (48.77 cents), or by the undecimal quarter tone, 33:32 (53.27 cents), approximately half the semitone of 16:15 or 25:24. The ratio of 36:35 is only 1.23 cents narrower than a 24-TET quarter tone. This just ratio is also the difference between a minor third (6:5) and septimal minor third (7:6).

Quarter tones and intervals close to them also occur in a number of other equally tempered tuning systems. 22-TET contains an interval of 54.55 cents, slightly wider than a quarter-tone, whereas 53-TET has an interval of 45.28 cents, slightly smaller. 72-TET also has equally tempered quarter-tones, and indeed contains 3 quarter tone scales, since 72 is divisible by 24. The smallest interval in 31 equal temperament (the "diesis" of 38.71 cents) is half a chromatic semitone, one-third of a diatonic semitone and one-fifth of a whole tone, so it may function as a quarter tone, a fifth-tone or a sixth-tone.

Composer Ben Johnston, to accommodate the just septimal quarter tone, uses a small "7" () as an accidental to indicate a note is lowered 49 cents, or an upside down "∠" () to indicate a note is raised 49 cents,[5] or a ratio of 36/35.[6] Johnston uses an upward and downward arrow to indicate a note is raised or lowered by a ratio of 33/32, or 53 cents.[6]

Playing quarter tones on musical instruments

A quarter tone clarinet by Fritz Schüller.

Because many musical instruments manufactured today are designed for the 12-tone scale, not all are usable for playing quarter tones. Sometimes special playing techniques must be used.

Conventional musical instruments that cannot play quarter tones (except by using special techniques—see below) include:

Conventional musical instruments that can play quarter tones include

Experimental instruments have been built to play in quarter tones; for example a quarter tone clarinet by Fritz Schüller (1883–1977) of Markneukirchen, and a quarter tone mechanism for flutes by Eva Kingma.

Other instruments can be used to play quarter tones when using audio signal processing effects such as pitch shifting.

Pairs of conventional instruments tuned a quarter tone apart can be used to play some quarter tone music. Indeed, quarter-tone pianos have been built, which consist essentially of two pianos stacked one above the other in a single case, one tuned a quarter tone higher than the other.

Music of the Middle East

Many Persian dastgah and Arabic maqamat contain intervals of three-quarter tone size; a short list of these follows.[7]

  1. Shoor (Bayati) 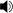 play 
    شور (بیاتی)
    D E F G A B♭ C D
  2. Rast 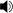 play 
    راست
    C D E F G A B C
    with a B♭ replacing the B in the descending scale
  3. Saba 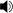 play 
    صبا
    D E F G♭ A B♭ C D
  4. Segah 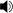 play 
    سه گاه
    E F G A B C D E
  5. ‘Ajam
  6. Hoseyni

The Islamic philosopher and scientist Al-Farabi described a number of intervals in his work in music, including a number of quarter tones.

Assyrian/Syriac Church Music Scale:[8]

Quarter tone scale

Quarter tone scale on C ascending and descending.  Play 
Composer Charles Ives chose the chord above as good possibility for a "secondary" chord in the quarter-tone scale, akin to the minor chord of traditional tonality. He considered that it may be built upon any degree of the quarter tone scale.[3]  Play 

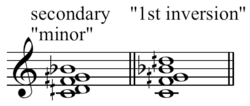
Known as gadwal in Arabic,[9] the quarter tone scale was developed in the Middle East in the eighteenth century and many of the first detailed writings in the nineteenth century Syria describe the scale as being of 24 equal tones.[10] The invention of the scale is attributed to Mikhail Mishaqa whose work Essay on the Art of Music for the Emir Shihāb (al-Risāla al-shihābiyya fi 'l-ṣinā‘a al-mūsīqiyya) is devoted to the topic but also makes clear his teacher Sheikh Muhammad al-‘Attār (1764-1828) was one of many already familiar with the concept.[11]

The quarter tone scale may be primarily a theoretical construct in Arabic music. The quarter tone gives musicians a "conceptual map" they can use to discuss and compare intervals by number of quarter tones, and this may be one of the reasons it accompanies a renewed interest in theory, with instruction in music theory a mainstream requirement since that period.[10]

Previously, pitches of a mode were chosen from a scale consisting of seventeen tones, developed by Safi 'I-Din al-Urmawi in the thirteenth century.[11]

The Japanese multi-instrumentalist and experimental musical instrument builder Yuichi Onoue developed a 24-TET quarter tone tuning on his guitar.[12] Norwegian guitarist Ronni Le Tekrø of the band TNT used a quarter-step guitar on the band's third studio album, Intuition.

Ancient Greek tetrachords

Greek Dorian enharmonic genus: two disjunct tetrachords each of a quarter tone, quarter tone, and major third.  Play 

The enharmonic genus of the Greek tetrachord consisted of a ditone or an approximate major third, and a semitone, which was divided into two microtones. Aristoxenos, Didymos and others presented the semitone as being divided into two approximate quarter tone intervals of about the same size, while other ancient Greek theorists described the microtones resulting from dividing the semitone of the enharmonic genus as unequal in size (i.e., one smaller than a quarter tone and one larger).[13]

Interval size in equal temperament

Here are the sizes of some common intervals in a 24-note equally tempered scale, with the interval names proposed by Alois Hába (neutral third, etc.) and Ivan Wyschnegradsky (major fourth, etc.):

interval name size (steps) size (cents) midi just ratio just (cents) midi error
octave 24 1200  play  2:1 1200.00  play  0.00
semidiminished octave 23 1150  play  35:18 1151.23  play  −1.23
supermajor seventh 23 1150  play  27:14 1137.03  play  +12.96
major seventh 22 1100  play  15:8 1088.27  play  +11.73
neutral seventh, major tone 21 1050  play  11:6 1049.36  play  +0.64
neutral seventh, minor tone 21 1050  play  20:11 1035.00  play  +15.00
large just minor seventh 20 1000  play  9:5 1017.60  play  −17.60
small just minor seventh 20 1000  play  16:9 996.09  play  +3.91
supermajor sixth/subminor seventh 19 950  play  7:4 968.83  play  −18.83
major sixth 18 900  play  5:3 884.36  play  +15.64
neutral sixth 17 850  play  18:11 852.59  play  −2.59
minor sixth 16 800  play  8:5 813.69  play  −13.69
subminor sixth 15 750  play  14:9 764.92  play  −14.92
perfect fifth 14 700  play  3:2 701.95  play  −1.95
minor fifth 13 650  play  16:11 648.68  play  +1.32
lesser septimal tritone 12 600  play  7:5 582.51  play  +17.49
major fourth 11 550  play  11:8 551.32  play  −1.32
perfect fourth 10 500  play  4:3 498.05  play  +1.95
tridecimal major third 9 450  play  13:10 454.21  play  −4.21
septimal major third 9 450  play  9:7 435.08  play  +14.92
major third 8 400  play  5:4 386.31  play  +13.69
undecimal neutral third 7 350  play  11:9 347.41  play  +2.59
minor third 6 300  play  6:5 315.64  play  −15.64
septimal minor third 5 250  play  7:6 266.88  play  −16.88
tridecimal minor third 5 250  play  15:13 247.74  play  +2.26
septimal whole tone 5 250  play  8:7 231.17  play  +18.83
major second, major tone 4 200  play  9:8 203.91  play  −3.91
major second, minor tone 4 200  play  10:9 182.40  play  +17.60
neutral second, greater undecimal 3 150  play  11:10 165.00  play  −15.00
neutral second, lesser undecimal 3 150  play  12:11 150.64  play  −0.64
15:14 semitone 2 100  play  15:14 119.44  play  −19.44
diatonic semitone, just 2 100  play  16:15 111.73  play  −11.73
21:20 semitone 2 100  play  21:20 84.47  play  +15.53
28:27 semitone 1 50  play  28:27 62.96  play  −12.96
septimal quarter tone 1 50  play  36:35 48.77  play  +1.23

Moving from 12-TET to 24-TET allows the better approximation of a number of intervals. Intervals matched particularly closely include the neutral second, neutral third, and (11:8) ratio, or the 11th harmonic. The septimal minor third and septimal major third are approximated rather poorly; the (13:10) and (15:13) ratios, involving the 13th harmonic, are matched very closely. Overall, 24-TET can be viewed as matching the 11th and 13th harmonics more closely than the 7th.

See also

References

  1. ↑ Touma, Habib Hassan (1996). The Music of the Arabs, p.16. Trans. Laurie Schwartz. Portland, Oregon: Amadeus Press. ISBN 0-931340-88-8.
  2. ↑ Julian Rushton., "Quarter-Tone", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan Publishers, 2001).
  3. 1 2 Boatwright, Howard (1965). "Ives' Quarter-Tone Impressions", Perspectives of New Music 3, no. 2 (Spring-Summer): pp. 22–31; citations on pp. 27–28; reprinted in Perspectives on American Composers, edited by Benjamin Boretz and Edward T. Cone, pp. 3-12, New York: W. W. Norton, 1971, citation on pp. 8–9. "These two chords outlined above might be termed major and minor."
  4. ↑ Julian Rushton, "Quarter-tone", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan Publishers, 2001).
  5. ↑ Douglas Keislar; Easley Blackwood; John Eaton; Lou Harrison; Ben Johnston; Joel Mandelbaum; William Schottstaedt. p.193. "Six American Composers on Nonstandard Tunnings", Perspectives of New Music, Vol. 29, No. 1. (Winter, 1991), pp. 176-211.
  6. 1 2 Fonville, John (Summer, 1991). "Ben Johnston's Extended Just Intonation: A Guide for Interpreters", p.114, Perspectives of New Music, Vol. 29, No. 2, pp. 106-137.
  7. ↑ Spector, Johanna (May 1970). "Classical 'Ud Music in Egypt with Special Reference to Maqamat". Ethnomusicology. 14 (2): 243–257. doi:10.2307/849799. JSTOR 00141836.
  8. ↑ Asaad, Gabriel (1990). Syria's Music Throughout History
  9. ↑ "Classical 'Ud Music in Egypt with Special Reference to Maqamat", p.246. Johanna Spector. Ethnomusicology, Vol. 14, No. 2. (May, 1970), pp. 243–57.
  10. 1 2 Marcus, Scott (1993)."The Interface between Theory and Practice: Intonation in Arab Music", Asian Music, Vol. 24, No. 2. (Spring - Summer, 1993), pp. 39–58.
  11. 1 2 Maalouf, Shireen (2003). "Mikhii'il Mishiiqa: Virtual Founder of the Twenty-Four Equal Quartertone Scale", Journal of the American Oriental Society, Vol. 123, No. 4. (Oct.–Dec., 2003), pp. 835–40.
  12. ↑ Yuichi Onoue on hypercustom.com Archived November 8, 2015, at the Wayback Machine.
  13. ↑ Chalmers, John H. Jr. (1993). Divisions of the Tetrachord. Hanover, NH: Frog Peak Music. ISBN 0-945996-04-7 Chapter 5, Page 49

Further reading

This article is issued from Wikipedia - version of the 11/28/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.