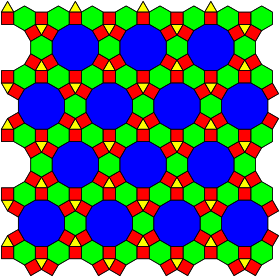
3-4-6-12 tiling
| 3-4-6-12 tiling | |
|---|---|
 | |
| Type | 2-uniform tiling |
| Vertex configuration | 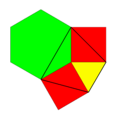 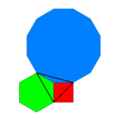 3.4.6.4 and 4.6.12 |
| Symmetry | p6m, [6,3], (*632) |
| Rotation symmetry | p6, [6,3]+, (632) |
| Properties | 2-uniform, 4-isohedral, 4-isotoxal |
In geometry of the Euclidean plane, the 3-4-6-12 tiling is one of 20 2-uniform tilings of the Euclidean plane by regular polygons, containing regular triangles, squares, hexagons and dodecagons, arranged in two vertex configuration: 3.4.6.4 and 4.6.12.[1][2][3][4]
It has hexagonal symmetry, p6m, [6,3], (*632). It is also called a demiregular tiling by some authors.
Geometry
Its two vertex configurations are shared with two 1-uniform tilings:
| rhombitrihexagonal tiling | truncated trihexagonal tiling |
|---|---|
 3.4.6.4 |
 4.6.12 |
It can be seen as a type of diminished rhombitrihexagonal tiling, with dodecagons replacing periodic sets of hexagons and surrounding squares and triangles. This is similar to the Johnson solid, a diminished rhombicosidodecahedron, which is a rhombicosidodecahedron with faces removed, leading to new decagonal faces.
Related k-uniform tilings of regular polygons
The hexagons can be dissected into 6 triangles, and the dodecagaons can be dissected into triangles, hexagons and squares.
 |
 |
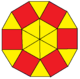 |
| Hexagon | Dodecagon (each has 2 orientations) | |
|---|---|---|
| 3-uniform tilings | ||
|---|---|---|
| 48 | 26 | 18 |
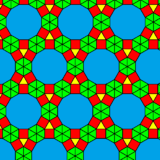 [36; 3.3.4.3.4; 3.3.4.12] |
 [3.4.4.6; (3.4.6.4)2] |
 [36; (3.3.4.3.4)2] |
Dual tiling
The dual tiling has right triangle and kite faces, defined by face configurations: V3.4.6.4 and V4.6.12, and can be seen combining the deltoidal trihexagonal tiling and kisrhombille tilings.
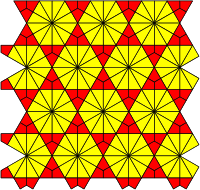 Dual tiling |
 V3.4.6.4  V4.6.12 |
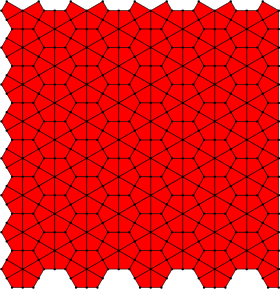 Deltoidal trihexagonal tiling |
 Kisrhombille tiling |
Notes
- ↑ Critchlow, p.62-67
- ↑ Grünbaum and Shephard 1986, pp. 65-67
- ↑ In Search of Demiregular Tilings #4
- ↑ Chavey (1989)
References
- Keith Critchlow, Order in Space: A design source book, 1970, pp. 62–67
- Ghyka, M. The Geometry of Art and Life, (1946), 2nd edition, New York: Dover, 1977. Demiregular tiling #15
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. pp. 35–43
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman. ISBN 0-7167-1193-1. p. 65
- Sacred Geometry Design Sourcebook: Universal Dimensional Patterns, Bruce Rawles, 1997. pp.36-37
External links
- Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
- Dutch, Steve. "Uniform Tilings". Retrieved 2006-09-09.
- Weisstein, Eric W. "Demiregular tessellation". MathWorld.
- In Search of Demiregular Tilings, Helmer Aslaksen
- n-uniform tilings Brian Galebach, 2-Uniform Tiling 1 of 20
