3-6 duoprism
Uniform 3-6 duoprisms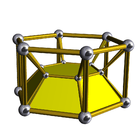 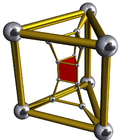 Schlegel diagrams | |
|---|---|
| Type | Prismatic uniform polychoron |
| Schläfli symbol | {3}×{6} |
| Coxeter–Dynkin diagram | |
| Cells | 3 hexagonal prisms, 6 triangular prisms |
| Faces | 12 squares, 3 hexagons, 6 triangles |
| Edges | 36 |
| Vertices | 18 |
| Vertex figure | Digonal disphenoid |
| Symmetry | [3,2,6], order 36 |
| Dual | 3-6 duopyramid |
| Properties | convex, vertex-uniform |
In geometry of 4 dimensions, a 3-6 duoprism, a duoprism and 4-polytope resulting from the Cartesian product of a triangle and a hexagon.
Images
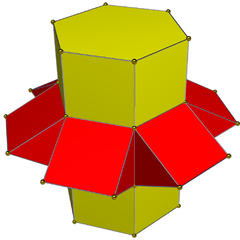 Net |
3-6 duopyramid
| dual uniform 3-6 duopyramid | |
|---|---|
| Type | duopyramid |
| Schläfli symbol | {3}+{6} |
| Coxeter-Dynkin diagram | |
| Cells | 18 digonal disphenoids |
| Faces | 36 isosceles triangles |
| Edges | 27 (18+3+6) |
| Vertices | 9 (3+6) |
| Symmetry | [3,2,6], order 36 |
| Dual | 3-6 duoprism |
| Properties | convex, facet-transitive |
The dual of a 3-6 duoprism is called a 3-6 duopyramid. It has 18 tetragonal disphenoid cells, 36 isosceles triangular faces, 27 edges, and 9 vertices.
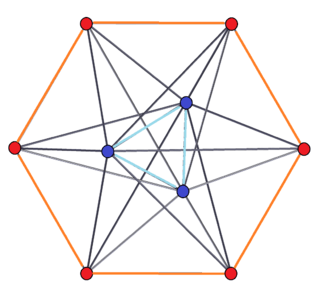
Orthogonal projection
See also
Notes
References
- Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
- Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
- Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33–62, 1937.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N. W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Olshevsky, George. "Duoprism". Glossary for Hyperspace. Archived from the original on 4 February 2007.
External links
- The Fourth Dimension Simply Explained—describes duoprisms as "double prisms" and duocylinders as "double cylinders"
- Polygloss – glossary of higher-dimensional terms
- Exploring Hyperspace with the Geometric Product
This article is issued from Wikipedia - version of the 12/8/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.