A-equivalence
In mathematics, 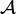 -equivalence, sometimes called right-left equivalence, is an equivalence relation between map germs.
-equivalence, sometimes called right-left equivalence, is an equivalence relation between map germs.
Let 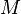 and
and 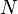 be two manifolds, and let
be two manifolds, and let 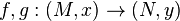 be two smooth map germs. We say that
be two smooth map germs. We say that 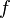 and
and 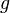 are
are 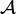 -equivalent if there exist diffeomorphism germs
-equivalent if there exist diffeomorphism germs 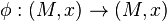 and
and 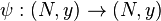 such that
such that 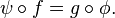
In other words, two map germs are 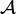 -equivalent if one can be taken onto the other by a diffeomorphic change of co-ordinates in the source (i.e.
-equivalent if one can be taken onto the other by a diffeomorphic change of co-ordinates in the source (i.e. 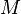 ) and the target (i.e.
) and the target (i.e. 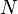 ).
).
Let 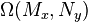 denote the space of smooth map germs
denote the space of smooth map germs 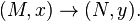 Let
Let 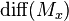 be the group of diffeomorphism germs
be the group of diffeomorphism germs 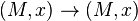 and
and
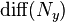 be the group of diffeomorphism germs
be the group of diffeomorphism germs 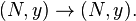 The group
The group 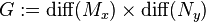 acts on
acts on 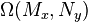 in the natural way:
in the natural way: 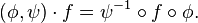 Under this action we see that the map germs
Under this action we see that the map germs 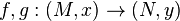 are
are 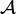 -equivalent if, and only if,
-equivalent if, and only if, 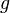 lies in the orbit of
lies in the orbit of 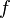 , i.e.
, i.e. 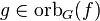 (or vice versa).
(or vice versa).
A map germ is called stable if its orbit under the action of 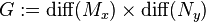 is open relative to the Whitney topology. Since
is open relative to the Whitney topology. Since 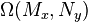 is an infinite dimensional space metric topology is no longer trivial. Whitney topology compares the differences in successive derivatives and gives a notion of proximity within the infinite dimensional space. A base for the open sets of the topology in question is given by taking
is an infinite dimensional space metric topology is no longer trivial. Whitney topology compares the differences in successive derivatives and gives a notion of proximity within the infinite dimensional space. A base for the open sets of the topology in question is given by taking 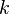 -jets for every
-jets for every 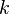 and taking open neighbourhoods in the ordinary Euclidean sense. Open sets in the topology are then unions of
these base sets.
and taking open neighbourhoods in the ordinary Euclidean sense. Open sets in the topology are then unions of
these base sets.
Consider the orbit of some map germ 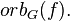 The map germ
The map germ 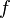 is called simple if there are only finitely many other orbits in a neighbourhood of each of its points. Vladimir Arnold has shown that the only simple singular map germs
is called simple if there are only finitely many other orbits in a neighbourhood of each of its points. Vladimir Arnold has shown that the only simple singular map germs 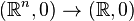 for
for 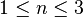 are the infinite sequence
are the infinite sequence 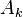 (
(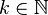 ), the infinite sequence
), the infinite sequence 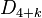 (
(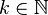 ),
), 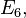
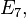 and
and 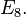
See also
- K-equivalence (contact equivalence)
References
- M. Golubitsky and V. Guillemin, Stable Mappings and Their Singularities. Graduate Texts in Mathematics, Springer.