Artin transfer (group theory)

In the mathematical field of group theory, an Artin transfer is a certain homomorphism from an arbitrary finite or infinite group to the commutator quotient group of a subgroup of finite index. Originally, such mappings arose as group theoretic counterparts of class extension homomorphisms of abelian extensions of algebraic number fields by applying Artin's reciprocity maps to ideal class groups and analyzing the resulting homomorphisms between quotients of Galois groups. However, independently of number theoretic applications, a partial order on the kernels and targets of Artin transfers has recently turned out to be compatible with parent-descendant relations between finite p-groups (with a prime number p), which can be visualized in descendant trees. Therefore, Artin transfers provide a valuable tool for the classification of finite p-groups and for searching and identifying particular groups in descendant trees by looking for patterns defined by the kernels and targets of Artin transfers. These strategies of pattern recognition are useful in purely group theoretic context, as well as for applications in algebraic number theory concerning Galois groups of higher p-class fields and Hilbert p-class field towers.

Transversals of a subgroup

Let $G$ be a group and $H\leq G$ be a subgroup of finite index ${\displaystyle n=(G:H)\geq 1}$.

Definitions. ^[1]

T

1. A left transversal of $H$ in $G$ is an ordered system $(g_{1},\ldots ,g_{n})$ of representatives for the left cosets of $H$ in $G$ such that $G={\dot {\bigcup }}_{{i=1}}^{n}\,g_{i}H$ is a disjoint union.
2. Similarly, a right transversal of $H$ in $G$ is an ordered system $(d_{1},\ldots ,d_{n})$ of representatives for the right cosets of $H$ in $G$ such that $G={\dot {\bigcup }}_{{i=1}}^{n}\,Hd_{i}$ is a disjoint union.

Remark. For any transversal of $H$ in $G$, there exists a unique subscript $1\leq i_{0}\leq n$ such that $g_{{i_{0}}}\in H$, resp. $d_{{i_{0}}}\in H$. Of course, this element with subscript $i_{0}$ which represents the principal coset (i.e., the subgroup $H$ itself) may be, but need not be, replaced by the neutral element $1$.

Lemma. ^[2]

1. If $G$ is non-abelian and $H$ is not a normal subgroup of $G$, then we can only say that the inverse elements $(g_{1}^{{-1}},\ldots ,g_{n}^{{-1}})$ of a left transversal $(g_{1},\ldots ,g_{n})$ form a right transversal of $H$ in $G$.
2. However, if $H\triangleleft G$ is a normal subgroup of $G$, then any left transversal is also a right transversal of $H$ in $G$.

For the proof click show on the right hand side.

Proof 

1. Since the mapping ${\displaystyle G\to G,\ x\mapsto x^{-1}}$ is an involution, that is a bijection which is its own inverse, we see that $G={\dot {\bigcup }}_{{i=1}}^{n}\,g_{i}H$ implies $G=G^{{-1}}={\dot {\bigcup }}_{{i=1}}^{n}\,(g_{i}H)^{{-1}}={\dot {\bigcup }}_{{i=1}}^{n}\,H^{{-1}}g_{i}^{{-1}}={\dot {\bigcup }}_{{i=1}}^{n}\,Hg_{i}^{{-1}}$.
2. For a normal subgroup $H\triangleleft G$, we have $xH=Hx$ for each $x\in G$.

Let ${\displaystyle \phi :\,G\to K}$ be a group homomorphism and $(g_{1},\ldots ,g_{n})$ be a left transversal of a subgroup $H$ in $G$ with finite index ${\displaystyle n=(G:H)\geq 1}$. We must check whether the image of this transversal under the homomorphism is again a transversal.

Proposition. The following two conditions are equivalent.

1. ${\displaystyle (\phi (g_{1}),\ldots ,\phi (g_{n}))}$ is a left transversal of the subgroup ${\displaystyle \phi (H)}$ in the image $\phi(G)$ with finite index ${\displaystyle (\phi (G):\phi (H))=n}$.
2. ${\displaystyle \ker(\phi )\leq H}$.

We emphasize this important equivalence in a formula:

${\displaystyle (1)\qquad \phi (G)={\dot {\bigcup }}_{i=1}^{n}\,\phi (g_{i})\phi (H)}$ and ${\displaystyle (\phi (G):\phi (H))=n\quad \Longleftrightarrow \quad \ker(\phi )\leq H}$.

For the proof click show on the right hand side.

Proof 

By assumption, we have the disjoint left coset decomposition $G={\dot {\bigcup }}_{{i=1}}^{n}\,g_{i}H$ which comprises two statements simultaneously.

Firstly, the group ${\displaystyle G=\bigcup _{i=1}^{n}\,g_{i}H}$ is a union of cosets, and secondly, any two distinct cosets have an empty intersection ${\displaystyle g_{i}H\bigcap g_{j}H=\emptyset }$, for $i\ne j$.

Due to the properties of the set mapping associated with $\phi$, the homomorphism $\phi$ maps the union to another union

${\displaystyle \phi (G)=\phi (\bigcup _{i=1}^{n}\,g_{i}H)=\bigcup _{i=1}^{n}\,\phi (g_{i}H)=\bigcup _{i=1}^{n}\,\phi (g_{i})\phi (H)}$,

but weakens the equality for the intersection to a trivial inclusion

${\displaystyle \emptyset =\phi (\emptyset )=\phi (g_{i}H\bigcap g_{j}H)\subseteq \phi (g_{i}H)\bigcap \phi (g_{j}H)=\phi (g_{i})\phi (H)\bigcap \phi (g_{j})\phi (H)}$, for $i\ne j$.

To show that the images of the cosets remain disjoint we need the property ${\displaystyle \ker(\phi )\leq H}$ of the homomorphism $\phi$.

Suppose that ${\displaystyle \phi (g_{i})\phi (H)\bigcap \phi (g_{j})\phi (H)\neq \emptyset }$ for some ${\displaystyle 1\leq i\leq j\leq n}$, then we have ${\displaystyle \phi (g_{i})\phi (h_{i})=\phi (g_{j})\phi (h_{j})}$ for certain elements ${\displaystyle h_{i},h_{j}\in H}$.

Multiplying by ${\displaystyle \phi (g_{j})^{-1}}$ from the left and by ${\displaystyle \phi (h_{j})^{-1}}$ from the right, we obtain

${\displaystyle \phi (g_{j}^{-1}g_{i}h_{i}h_{j}^{-1})=\phi (g_{j})^{-1}\phi (g_{i})\phi (h_{i})\phi (h_{j})^{-1}=1}$, that is, ${\displaystyle g_{j}^{-1}g_{i}h_{i}h_{j}^{-1}\in \ker(\phi )\leq H}$.

Since ${\displaystyle h_{i}h_{j}^{-1}\in H}$, this implies ${\displaystyle g_{j}^{-1}g_{i}\in H}$, resp. ${\displaystyle g_{i}H=g_{j}H}$, and thus $i=j$.

Conversely, we use contraposition.

If the kernel $\ker(\phi)$ of $\phi$ is not contained in the subgroup $H$, then there exists an element $x\in G\setminus H$ such that ${\displaystyle \phi (x)=1}$.

But then the homomorphism $\phi$ maps the disjoint cosets ${\displaystyle xH\bigcap 1\cdot H=\emptyset }$ to equal cosets ${\displaystyle \phi (x)\phi (H)\bigcap \phi (1)\phi (H)=1\cdot \phi (H)\bigcap 1\cdot \phi (H)=\phi (H)}$.

Permutation representation

Suppose $(g_{1},\ldots ,g_{n})$ is a left transversal of a subgroup $H\leq G$ of finite index ${\displaystyle n=(G:H)\geq 1}$ in a group $G$. A fixed element $x\in G$ gives rise to a unique permutation $\pi _{x}\in S_{n}$ of the left cosets of $H$ in $G$ by left multiplication such that

${\displaystyle (2)\qquad xg_{i}H=g_{\pi _{x}(i)}H,\qquad {\text{ resp. }}xg_{i}\in g_{\pi _{x}(i)}H,\qquad {\text{ resp. }}u_{x}(i):=g_{\pi _{x}(i)}^{-1}xg_{i}\in H}$, for each $1\leq i\leq n$.

Similarly, if $(d_{1},\ldots ,d_{n})$ is a right transversal of $H$ in $G$, then a fixed element $x\in G$ gives rise to a unique permutation $\rho _{x}\in S_{n}$ of the right cosets of $H$ in $G$ by right multiplication such that

${\displaystyle (3)\qquad Hd_{i}x=Hd_{\rho _{x}(i)},\qquad {\text{ resp. }}d_{i}x\in Hd_{\rho _{x}(i)},\qquad {\text{ resp. }}w_{x}(i):=d_{i}xd_{\rho _{x}(i)}^{-1}\in H}$, for each $1\leq i\leq n$.

The elements ${\displaystyle u_{x}(i)}$, resp. ${\displaystyle w_{x}(i)}$, $1\leq i\leq n$, of the subgroup $H$ are called the monomials associated with $x$ with respect to $(g_{1},\ldots ,g_{n})$, resp. $(d_{1},\ldots ,d_{n})$.

Definitions. ^[1]

The mapping $G\to S_{n},\ x\mapsto \pi _{x}$, resp. ${\displaystyle G\to S_{n},\ x\mapsto \rho _{x}}$, is called the permutation representation of $G$ in the symmetric group $S_{n}$ with respect to $(g_{1},\ldots ,g_{n})$, resp. $(d_{1},\ldots ,d_{n})$.

The mapping ${\displaystyle G\to H^{n}\times S_{n},\ x\mapsto (u_{x}(1),\ldots ,u_{x}(n);\pi _{x})}$, resp. ${\displaystyle G\to H^{n}\times S_{n},\ x\mapsto (w_{x}(1),\ldots ,w_{x}(n);\rho _{x})}$, is called the monomial representation of $G$ in $H^{n}\times S_{n}$ with respect to $(g_{1},\ldots ,g_{n})$, resp. $(d_{1},\ldots ,d_{n})$.

Lemma. For the special right transversal $(g_{1}^{{-1}},\ldots ,g_{n}^{{-1}})$ associated to the left transversal $(g_{1},\ldots ,g_{n})$, we have the following relations between the monomials and permutations corresponding to an element $x\in G$:

${\displaystyle (4)\qquad w_{x^{-1}}(i)=u_{x}(i)^{-1}}$ for ${\displaystyle 1\leq i\leq n\qquad {\text{ and }}\qquad \rho _{x^{-1}}=\pi _{x}}$.

For the proof click show on the right hand side.

Proof 

For the right transversal $(g_{1}^{{-1}},\ldots ,g_{n}^{{-1}})$, we have ${\displaystyle w_{x}(i)=g_{i}^{-1}xg_{\rho _{x}(i)}}$, for each $1\leq i\leq n$. On the other hand, for the left transversal $(g_{1},\ldots ,g_{n})$, we have ${\displaystyle u_{x}(i)^{-1}=(g_{\pi _{x}(i)}^{-1}xg_{i})^{-1}=g_{i}^{-1}x^{-1}g_{\pi _{x}(i)}=g_{i}^{-1}x^{-1}g_{\rho _{x^{-1}}(i)}=w_{x^{-1}}(i)}$, for each $1\leq i\leq n$. This relation simultaneously shows that, for any $x\in G$, the permutation representations and the associated monomials are connected by

$\rho _{{x^{{-1}}}}=\pi _{x}$ and ${\displaystyle w_{x^{-1}}(i)=u_{x}(i)^{-1}}$ for each $1\leq i\leq n$.

Artin transfer

Let $G$ be a group and $H\leq G$ be a subgroup of finite index ${\displaystyle n=(G:H)\geq 1}$. Assume that $(g_{1},\ldots ,g_{n})$, resp. $(d_{1},\ldots ,d_{n})$, is a left, resp. right, transversal of $H$ in $G$ with associated permutation representation $G\to S_{n},\ x\mapsto \pi _{x}$, resp. ${\displaystyle \rho _{x}}$, such that ${\displaystyle u_{x}(i):=g_{\pi _{x}(i)}^{-1}xg_{i}\in H}$, resp. ${\displaystyle w_{x}(i):=d_{i}xd_{\rho _{x}(i)}^{-1}\in H}$, for $1\leq i\leq n$.

Definitions. ^{[2] [3]}

The Artin transfer $T_{{G,H}}:\ G\to H/H^{\prime }$ from $G$ to the abelianization $H/H^{\prime }$ of $H$ with respect to $(g_{1},\ldots ,g_{n})$, resp. $(d_{1},\ldots ,d_{n})$, is defined by

${\displaystyle (5)\qquad T_{G,H}^{(g)}(x):=\prod _{i=1}^{n}\,g_{\pi _{x}(i)}^{-1}xg_{i}\cdot H^{\prime }\qquad {\text{ briefly }}T_{G,H}(x)=\prod _{i=1}^{n}\,u_{x}(i)\cdot H^{\prime }}$,

resp.

${\displaystyle (6)\qquad T_{G,H}^{(d)}(x):=\prod _{i=1}^{n}\,d_{i}xd_{\rho _{x}(i)}^{-1}\cdot H^{\prime }\qquad {\text{ briefly }}T_{G,H}(x)=\prod _{i=1}^{n}\,w_{x}(i)\cdot H^{\prime }}$,

for $x\in G$.

Remarks. Isaacs ^[4] calls the mapping ${\displaystyle P:\,G\to H}$, ${\displaystyle x\mapsto \prod _{i=1}^{n}\,u_{x}(i)}$, resp. ${\displaystyle x\mapsto \prod _{i=1}^{n}\,w_{x}(i)}$, the pre-transfer from $G$ to $H$. The pre-transfer can be composed with a homomorphism ${\displaystyle \phi :\,H\to A}$ from $H$ into an abelian group $A$ to define a more general version of the transfer ${\displaystyle (\phi \circ P):\,G\to A}$, ${\displaystyle x\mapsto \prod _{i=1}^{n}\,\phi (u_{x}(i))}$, resp. ${\displaystyle x\mapsto \prod _{i=1}^{n}\,\phi (w_{x}(i))}$, from $G$ to $A$ via $\phi$, which occurs in the book by Gorenstein. ^[5] Taking the natural epimorphism ${\displaystyle \phi :\,H\to H/H^{\prime }}$, ${\displaystyle v\mapsto vH^{\prime }}$, yields the preceding Definition of the Artin transfer $T_{{G,H}}$ in its original form by Schur ^[2] and by Emil Artin, ^[3] which has also been dubbed Verlagerung by Hasse. ^[6] Note that, in general, the pre-transfer is neither independent of the transversal nor a group homomorphism.

Independence of the transversal

Assume that ${\displaystyle (\ell _{1},\ldots ,\ell _{n})}$ is another left transversal of $H$ in $G$ such that ${\displaystyle G={\dot {\cup }}_{i=1}^{n}\,\ell _{i}H}$.

Proposition. ^{[1] [2] [4] [5] [7] [8] [9]} The Artin transfers with respect to ${\displaystyle (\ell )}$ and ${\displaystyle (g)}$ coincide, that is, ${\displaystyle T_{G,H}^{(\ell )}=T_{G,H}^{(g)}}$.

For the proof click show on the right hand side.

Proof 

There exists a unique permutation $\sigma \in S_{n}$ such that ${\displaystyle g_{i}H=\ell _{\sigma (i)}H}$, for all $1\leq i\leq n$. Consequently, ${\displaystyle h_{i}:=g_{i}^{-1}\ell _{\sigma (i)}\in H}$, resp. ${\displaystyle \ell _{\sigma (i)}=g_{i}h_{i}}$ with $h_{i}\in H$, for all $1\leq i\leq n$. For a fixed element $x\in G$, there exists a unique permutation $\lambda _{x}\in S_{n}$ such that we have

${\displaystyle \ell _{\lambda _{x}(\sigma (i))}H=x\ell _{\sigma (i)}H=xg_{i}h_{i}H=xg_{i}H=g_{\pi _{x}(i)}H=g_{\pi _{x}(i)}h_{\pi _{x}(i)}H=\ell _{\sigma (\pi _{x}(i))}H}$,

for all $1\leq i\leq n$. Therefore, the permutation representation of $G$ with respect to ${\displaystyle (\ell _{1},\ldots ,\ell _{n})}$ is given by $\lambda _{x}\circ \sigma =\sigma \circ \pi _{x}$, resp. $\lambda _{x}=\sigma \circ \pi _{x}\circ \sigma ^{{-1}}\in S_{n}$, for $x\in G$. Furthermore, for the connection between the elements ${\displaystyle v_{x}(i):=\ell _{\lambda _{x}(i)}^{-1}x\ell _{i}\in H}$ and ${\displaystyle u_{x}(i):=g_{\pi _{x}(i)}^{-1}xg_{i}\in H}$, we obtain

${\displaystyle v_{x}(\sigma (i))=\ell _{\lambda _{x}(\sigma (i))}^{-1}x\ell _{\sigma (i)}=\ell _{\sigma (\pi _{x}(i))}^{-1}xg_{i}h_{i}}$

${\displaystyle =(g_{\pi _{x}(i)}h_{\pi _{x}(i)})^{-1}xg_{i}h_{i}=h_{\pi _{x}(i)}^{-1}g_{\pi _{x}(i)}^{-1}xg_{i}h_{i}=h_{\pi _{x}(i)}^{-1}u_{x}(i)h_{i}}$,

for all $1\leq i\leq n$. Finally, due to the commutativity of the quotient group $H/H^{\prime }$ and the fact that $\sigma$ and $\pi _{x}$ are permutations, the Artin transfer turns out to be independent of the left transversal:

${\displaystyle T_{G,H}^{(\ell )}(x)=\prod _{i=1}^{n}\,v_{x}(\sigma (i))\cdot H^{\prime }=\prod _{i=1}^{n}\,h_{\pi _{x}(i)}^{-1}u_{x}(i)h_{i}\cdot H^{\prime }}$

${\displaystyle =\prod _{i=1}^{n}\,u_{x}(i)\prod _{i=1}^{n}\,h_{\pi _{x}(i)}^{-1}\prod _{i=1}^{n}\,h_{i}\cdot H^{\prime }}$

${\displaystyle =\prod _{i=1}^{n}\,u_{x}(i)\cdot 1\cdot H^{\prime }=\prod _{i=1}^{n}\,u_{x}(i)\cdot H^{\prime }=T_{G,H}^{(g)}(x)}$,

as defined in formula (5).

It is clear that a similar proof shows that the Artin transfer is independent of the choice between two different right transversals. It remains to show that the Artin transfer with respect to a right transversal coincides with the Artin transfer with respect to a left transversal.

For this purpose, we select the special right transversal $(g_{1}^{{-1}},\ldots ,g_{n}^{{-1}})$ associated to the left transversal $(g_{1},\ldots ,g_{n})$.

Proposition. The Artin transfers with respect to ${\displaystyle (g^{-1})}$ and ${\displaystyle (g)}$ coincide, that is, ${\displaystyle T_{G,H}^{(g^{-1})}=T_{G,H}^{(g)}}$.

For the proof click show on the right hand side.

Proof 

Using the commutativity of $H/H^{\prime }$ and formula (4), we consider the expression

${\displaystyle T_{G,H}^{(g^{-1})}(x)=\prod _{i=1}^{n}\,g_{i}^{-1}xg_{\rho _{x}(i)}\cdot H^{\prime }=\prod _{i=1}^{n}\,w_{x}(i)\cdot H^{\prime }}$

${\displaystyle =\prod _{i=1}^{n}\,u_{x^{-1}}(i)^{-1}\cdot H^{\prime }=(\prod _{i=1}^{n}\,u_{x^{-1}}(i)\cdot H^{\prime })^{-1}}$

$=(T_{{G,H}}^{{(g)}}(x^{{-1}}))^{{-1}}=T_{{G,H}}^{{(g)}}(x)$.

The last step is justified by the fact that the Artin transfer is a homomorphism. This will be shown in the following section.

Artin transfers as homomorphisms

Let$(g_{1},\ldots ,g_{n})$ be a left transversal of $H$ in $G$.

Theorem. ^{[1] [2] [4] [5] [7] [8] [9]} The Artin transfer ${\displaystyle T_{G,H}:\,G\to H/H^{\prime },\ x\mapsto \prod _{i=1}^{n}\,g_{\pi _{x}(i)}^{-1}xg_{i}\cdot H^{\prime }}$ and the permutation representation $G\to S_{n},\ x\mapsto \pi _{x}$ are group homomorphisms:

${\displaystyle (7)\qquad T_{G,H}(xy)=T_{G,H}(x)\cdot T_{G,H}(y){\text{ and }}\pi _{xy}=\pi _{x}\circ \pi _{y}{\text{ for }}x,y\in G}$.

For the proof click show on the right hand side.

Proof 

Let $x,y\in G$ be two elements with transfer images

$T_{{G,H}}(x)=\prod _{{i=1}}^{n}\,g_{{\pi _{x}(i)}}^{{-1}}xg_{i}\cdot H^{\prime }$ and

$T_{{G,H}}(y)=\prod _{{j=1}}^{n}\,g_{{\pi _{y}(j)}}^{{-1}}yg_{j}\cdot H^{\prime }$.

Since $H/H^{\prime }$ is abelian and $\pi _{y}$ is a permutation, we can change the order of the factors in the following product:

${\displaystyle T_{G,H}(x)\cdot T_{G,H}(y)=\prod _{i=1}^{n}\,g_{\pi _{x}(i)}^{-1}xg_{i}H^{\prime }\cdot \prod _{j=1}^{n}\,g_{\pi _{y}(j)}^{-1}yg_{j}\cdot H^{\prime }}$

${\displaystyle =\prod _{j=1}^{n}\,g_{\pi _{x}(\pi _{y}(j))}^{-1}xg_{\pi _{y}(j)}H^{\prime }\cdot \prod _{j=1}^{n}\,g_{\pi _{y}(j)}^{-1}yg_{j}\cdot H^{\prime }}$

${\displaystyle =\prod _{j=1}^{n}\,g_{\pi _{x}(\pi _{y}(j))}^{-1}xg_{\pi _{y}(j)}g_{\pi _{y}(j)}^{-1}yg_{j}\cdot H^{\prime }}$

${\displaystyle =\prod _{j=1}^{n}\,g_{(\pi _{x}\circ \pi _{y})(j))}^{-1}xyg_{j}\cdot H^{\prime }=T_{G,H}(xy)}$.

This relation simultaneously shows that the Artin transfer $T_{{G,H}}$ and the permutation representation $G\to S_{n},\ x\mapsto \pi _{x}$ are homomorphisms, since ${\displaystyle T_{G,H}(xy)=T_{G,H}(x)\cdot T_{G,H}(y)}$ and $\pi _{{xy}}=\pi _{x}\circ \pi _{y}$.

It is illuminating to restate the homomorphism property of the Artin transfer in terms of the monomial representation. The images of the factors $x,y$ are given by ${\displaystyle T_{G,H}(x)=\prod _{i=1}^{n}\,u_{x}(i)\cdot H^{\prime }}$ and ${\displaystyle T_{G,H}(y)=\prod _{j=1}^{n}\,u_{y}(j)\cdot H^{\prime }}$. In the last proof, the image of the product $xy$ turned out to be

${\displaystyle T_{G,H}(xy)=\prod _{j=1}^{n}\,g_{\pi _{x}(\pi _{y}(j))}^{-1}xg_{\pi _{y}(j)}g_{\pi _{y}(j)}^{-1}yg_{j}\cdot H^{\prime }=\prod _{j=1}^{n}\,u_{x}(\pi _{y}(j))\cdot u_{y}(j)\cdot H^{\prime }}$,

which is a very peculiar law of composition discussed in more detail in the following section.

The law reminds of the crossed homomorphisms ${\displaystyle x\mapsto u_{x}}$ in the first cohomology group ${\mathrm {H}}^{1}(G,M)$ of a $G$-module $M$, which have the property ${\displaystyle u_{xy}=u_{x}^{y}\cdot u_{y}}$ for $x,y\in G$.

Wreath product of H and S(n)

The peculiar structures which arose in the previous section can also be interpreted by endowing the cartesian product $H^{n}\times S_{n}$ with a special law of composition known as the wreath product $H\wr S_{n}$ of the groups $H$ and $S_{n}$ with respect to the set $\lbrace 1,\ldots ,n\rbrace$.

Definition. For $x,y\in G$, the wreath product of the associated monomials and permutations is given by

${\displaystyle (8)\qquad (u_{x}(1),\ldots ,u_{x}(n);\pi _{x})\cdot (u_{y}(1),\ldots ,u_{y}(n);\pi _{y})}$

${\displaystyle :=(u_{x}(\pi _{y}(1))\cdot u_{y}(1),\ldots ,u_{x}(\pi _{y}(n))\cdot u_{y}(n);\pi _{x}\circ \pi _{y})}$

${\displaystyle =(u_{xy}(1),\ldots ,u_{xy}(n);\pi _{xy})}$.

Theorem. ^{[1] [7]} This law of composition on $H^{n}\times S_{n}$ causes the monomial representation ${\displaystyle G\to H\wr S_{n},\ x\mapsto (u_{x}(1),\ldots ,u_{x}(n);\pi _{x})}$ also to be a homomorphism. In fact, it is an injective homomorphism, also called a monomorphism or embedding, in contrast to the permutation representation, which cannot be injective if $G$ is infinite or at least of an order bigger than $n!$, the factorial.

For the proof click show on the right hand side.

Proof 

The homomorphism property has been shown above already. For a homomorphism to be injective, it suffices to show the triviality of its kernel. The neutral element of the group $H^{n}\times S_{n}$ endowed with the wreath product is given by ${\displaystyle (1,\ldots ,1;1)}$, where the last $1$ means the identity permutation. If ${\displaystyle (u_{x}(1),\ldots ,u_{x}(n);\pi _{x})=(1,\ldots ,1;1)}$, for some $x\in G$, then ${\displaystyle \pi _{x}=1}$ and consequently ${\displaystyle 1=u_{x}(i)=g_{\pi _{x}(i)}^{-1}xg_{i}=g_{i}^{-1}xg_{i}}$, for all $1\leq i\leq n$. Finally, an application of the inverse inner automorphism with $g_{i}$ yields $x=1$, as required for injectivity.

Whereas Huppert^[1] uses the monomial representation for defining the Artin transfer, we prefer to give the immediate definitions in formulas (5) and (6) and to merely illustrate the homomorphism property of the Artin transfer with the aid of the monomial representation.

Composition of Artin transfers

Let $G$ be a group with nested subgroups $K\leq H\leq G$ such that the indices ${\displaystyle (G:H)=n}$, ${\displaystyle (H:K)=m}$ and $(G:K)=(G:H)\cdot (H:K)=n\cdot m$ are finite.

Theorem. ^{[1] [7]} Then the Artin transfer $T_{{G,K}}$ is the compositum of the induced transfer ${\tilde {T}}_{{H,K}}:\ H/H^{\prime }\to K/K^{\prime }$ and the Artin transfer $T_{{G,H}}$, that is,

${\displaystyle (9)\qquad T_{G,K}={\tilde {T}}_{H,K}\circ T_{G,H}}$.

For the proof click show on the right hand side.

Proof 

This claim can be seen in the following manner.

If $(g_{1},\ldots ,g_{n})$ is a left transversal of $H$ in $G$ and $(h_{1},\ldots ,h_{m})$ is a left transversal of $K$ in $H$,

that is $G={\dot {\cup }}_{{i=1}}^{n}\,g_{i}H$ and $H={\dot {\cup }}_{{j=1}}^{m}\,h_{j}K$, then

$G={\dot {\cup }}_{{i=1}}^{n}\,{\dot {\cup }}_{{j=1}}^{m}\,g_{i}h_{j}K$

is a disjoint left coset decomposition of $G$ with respect to $K$.

Given two elements $x\in G$ and $y\in H$, there exist unique permutations $\pi _{x}\in S_{n}$, and $\sigma _{y}\in S_{m}$, such that

${\displaystyle u_{x}(i):=g_{\pi _{x}(i)}^{-1}xg_{i}\in H}$, for each $1\leq i\leq n$, and

${\displaystyle v_{y}(j):=h_{\sigma _{y}(j)}^{-1}yh_{j}\in K}$, for each $1\leq j\leq m$.

Then, anticipating the definition of the induced transfer, we have

${\displaystyle T_{G,H}(x)=\prod _{i=1}^{n}\,u_{x}(i)\cdot H^{\prime }}$, and ${\displaystyle {\tilde {T}}_{H,K}(y\cdot H^{\prime })=T_{H,K}(y)=\prod _{j=1}^{m}\,v_{y}(j)\cdot K^{\prime }}$.

For each pair of subscripts $1\leq i\leq n$ and $1\leq j\leq m$, we put ${\displaystyle y_{i}:=u_{x}(i)}$, and we obtain

${\displaystyle xg_{i}h_{j}=g_{\pi _{x}(i)}g_{\pi _{x}(i)}^{-1}xg_{i}h_{j}=g_{\pi _{x}(i)}u_{x}(i)h_{j}=g_{\pi _{x}(i)}y_{i}h_{j}}$

${\displaystyle =g_{\pi _{x}(i)}h_{\sigma _{y_{i}}(j)}h_{\sigma _{y_{i}}(j)}^{-1}y_{i}h_{j}=g_{\pi _{x}(i)}h_{\sigma _{y_{i}}(j)}v_{y_{i}}(j)}$,

resp. ${\displaystyle h_{\sigma _{y_{i}}(j)}^{-1}g_{\pi _{x}(i)}^{-1}xg_{i}h_{j}=v_{y_{i}}(j)}$.

Therefore, the image of $x$ under the Artin transfer $T_{{G,K}}$ is given by

${\displaystyle T_{G,K}(x)=\prod _{i=1}^{n}\,\prod _{j=1}^{m}\,v_{y_{i}}(j)\cdot K^{\prime }=\prod _{i=1}^{n}\,\prod _{j=1}^{m}\,h_{\sigma _{y_{i}}(j)}^{-1}g_{\pi _{x}(i)}^{-1}xg_{i}h_{j}\cdot K^{\prime }}$

${\displaystyle =\prod _{i=1}^{n}\,\prod _{j=1}^{m}\,h_{\sigma _{y_{i}}(j)}^{-1}u_{x}(i)h_{j}\cdot K^{\prime }=\prod _{i=1}^{n}\,\prod _{j=1}^{m}\,h_{\sigma _{y_{i}}(j)}^{-1}y_{i}h_{j}\cdot K^{\prime }}$

${\displaystyle =\prod _{i=1}^{n}\,{\tilde {T}}_{H,K}(y_{i}\cdot H^{\prime })={\tilde {T}}_{H,K}(\prod _{i=1}^{n}\,y_{i}\cdot H^{\prime })={\tilde {T}}_{H,K}(\prod _{i=1}^{n}\,u_{x}(i)\cdot H^{\prime })}$

${\displaystyle ={\tilde {T}}_{H,K}(T_{G,H}(x))}$.

Finally, we want to emphasize the structural peculiarity of the monomial representation

$G\to K^{{n\cdot m}}\times S_{{n\cdot m}}$, ${\displaystyle x\mapsto (k_{x}(1,1),\ldots ,k_{x}(n,m);\gamma _{x})}$,

which corresponds to the composite of Artin transfers, defining ${\displaystyle k_{x}(i,j):=((gh)_{\gamma _{x}(i,j)})^{-1}x(gh)_{(i,j)}\in K}$ for a permutation $\gamma _{x}\in S_{{n\cdot m}}$, and using the symbolic notation $(gh)_{{(i,j)}}:=g_{i}h_{j}$ for all pairs of subscripts $1\leq i\leq n$, $1\leq j\leq m$.

The preceding proof has shown that ${\displaystyle k_{x}(i,j)=h_{\sigma _{y_{i}}(j)}^{-1}g_{\pi _{x}(i)}^{-1}xg_{i}h_{j}}$. Therefore, the action of the permutation $\gamma _{x}$ on the set $\lbrack 1,n\rbrack \times \lbrack 1,m\rbrack$ is given by ${\displaystyle \gamma _{x}(i,j)=(\pi _{x}(i),\sigma _{u_{x}(i)}(j))}$. The action on the second component $j$ depends on the first component $i$ (via the permutation ${\displaystyle \sigma _{u_{x}(i)}\in S_{m}}$), whereas the action on the first component $i$ is independent of the second component $j$. Therefore, the permutation $\gamma _{x}\in S_{{n\cdot m}}$ can be identified with the multiplet

${\displaystyle (\pi _{x};\sigma _{u_{x}(1)},\ldots ,\sigma _{u_{x}(n)})\in S_{n}\times S_{m}^{n},}$

which will be written in twisted form in the next section.

Wreath product of S(m) and S(n)

The permutations $\gamma _{x}$, which arose as second components of the monomial representation

${\displaystyle G\to K\wr S_{n\cdot m}}$, ${\displaystyle x\mapsto (k_{x}(1,1),\ldots ,k_{x}(n,m);\gamma _{x})}$,

in the previous section, are of a very special kind. They belong to the stabilizer of the natural equipartition of the set $\lbrack 1,n\rbrack \times \lbrack 1,m\rbrack$ into the $n$ rows of the corresponding matrix (rectangular array). Using the peculiarities of the composition of Artin transfers in the previous section, we show that this stabilizer is isomorphic to the wreath product $S_{m}\wr S_{n}$ of the symmetric groups $S_m$ and $S_{n}$ with respect to the set $\lbrace 1,\ldots ,n\rbrace$, whose underlying set $S_{m}^{n}\times S_{n}$ is endowed with the following law of composition

${\displaystyle (10)\qquad \gamma _{x}\cdot \gamma _{z}=(\sigma _{u_{x}(1)},\ldots ,\sigma _{u_{x}(n)};\pi _{x})\cdot (\sigma _{u_{z}(1)},\ldots ,\sigma _{u_{z}(n)};\pi _{z})}$

${\displaystyle =(\sigma _{u_{x}(\pi _{z}(1))}\circ \sigma _{u_{z}(1)},\ldots ,\sigma _{u_{x}(\pi _{z}(n))}\circ \sigma _{u_{z}(n)};\pi _{x}\circ \pi _{z})}$

${\displaystyle =(\sigma _{u_{xz}(1)},\ldots ,\sigma _{u_{xz}(n)};\pi _{xz})}$

$=\gamma _{{xz}}$ for all $x,z\in G$.

This law reminds of the chain rule $D(g\circ f)(x)=D(g)(f(x))\circ D(f)(x)$ for the Fréchet derivative in $x\in E$ of the compositum of differentiable functions $f:\,E\to F$ and $g:\,F\to G$ between complete normed spaces.

The above considerations establish a third representation, the stabilizer representation,

${\displaystyle G\to S_{m}\wr S_{n},\ x\mapsto (\sigma _{u_{x}(1)},\ldots ,\sigma _{u_{x}(n)};\pi _{x})}$

of the group $G$ in the wreath product $S_{m}\wr S_{n}$, similar to the permutation representation and the monomial representation. As opposed to the latter, the stabilizer representation cannot be injective, in general. For instance, certainly not, if $G$ is infinite. Formula (10) proves the following statement.

Theorem. The stabilizer representation ${\displaystyle G\to S_{m}\wr S_{n},\ x\mapsto \gamma _{x}=(\sigma _{u_{x}(1)},\ldots ,\sigma _{u_{x}(n)};\pi _{x})}$ of the group $G$ in the wreath product $S_{m}\wr S_{n}$ of symmetric groups is a group homomorphism.

Cycle decomposition

Let $(g_{1},\ldots ,g_{n})$ be a left transversal of a subgroup $H\leq G$ of finite index ${\displaystyle n=(G:H)\geq 1}$ in a group $G$. Suppose the element $x\in G$ gives rise to the permutation $\pi _{x}\in S_{n}$ of the left cosets of $H$ in $G$ such that $xg_{i}H=g_{{\pi _{x}(i)}}H$, resp. ${\displaystyle g_{\pi _{x}(i)}^{-1}xg_{i}=:u_{x}(i)\in H}$, for each $1\leq i\leq n$.

Theorem. ^{[1] [3] [4] [5] [8] [9]} If the permutation $\pi _{x}$ has the decomposition $\pi _{x}=\prod _{{j=1}}^{t}\,\zeta _{j}$ into pairwise disjoint (and thus commuting) cycles $\zeta _{j}\in S_{n}$ of lengths $f_{j}\geq 1$, which is unique up to the ordering of the cycles, more explicitly, if

${\displaystyle (11)\qquad (g_{j}H,g_{\zeta _{j}(j)}H,g_{\zeta _{j}^{2}(j)}H,\ldots ,g_{\zeta _{j}^{f_{j}-1}(j)}H)=(g_{j}H,xg_{j}H,x^{2}g_{j}H,\ldots ,x^{f_{j}-1}g_{j}H)}$,

for $1\leq j\leq t$, and $\sum _{{j=1}}^{t}\,f_{j}=n$, then the image of $x\in G$ under the Artin transfer $T_{{G,H}}$ is given by

${\displaystyle (12)\qquad T_{G,H}(x)=\prod _{j=1}^{t}\,g_{j}^{-1}x^{f_{j}}g_{j}\cdot H^{\prime }}$.

For the proof click show on the right hand side.

Proof 

The reason for this fact is that we obtain another left transversal of $H$ in $G$ by putting ${\displaystyle \ell _{j,k}:=x^{k}g_{j}}$ for $0\leq k\leq f_{j}-1$ and $1\leq j\leq t$, since

${\displaystyle (13)\qquad G={\dot {\cup }}_{j=1}^{t}\,{\dot {\cup }}_{k=0}^{f_{j}-1}\,x^{k}g_{j}H}$

is a disjoint decomposition of $G$ into left cosets of $H$.

Let us fix a value of $1\leq j\leq t$. For $0\leq k\leq f_{j}-2$, we have

${\displaystyle x\ell _{j,k}=xx^{k}g_{j}=x^{k+1}g_{j}=\ell _{j,k+1}\in \ell _{j,k+1}H}$, resp. ${\displaystyle u_{x}(j,k):=\ell _{j,k+1}^{-1}x\ell _{j,k}=1\in H}$.

However, for $k=f_{j}-1$, we obtain

${\displaystyle x\ell _{j,f_{j}-1}=xx^{f_{j}-1}g_{j}=x^{f_{j}}g_{j}\in g_{j}H=\ell _{j,0}H}$, resp. ${\displaystyle u_{x}(j,f_{j}-1):=\ell _{j,0}^{-1}x\ell _{j,f_{j}-1}=g_{j}^{-1}x^{f_{j}}g_{j}\in H}$.

Consequently,

${\displaystyle T_{G,H}(x)=\prod _{j=1}^{t}\,\prod _{k=0}^{f_{j}-1}\,u_{x}(j,k)\cdot H^{\prime }=\prod _{j=1}^{t}\,(\prod _{k=0}^{f_{j}-2}\,1)\cdot u_{x}(j,f_{j}-1)\cdot H^{\prime }=\prod _{j=1}^{t}\,g_{j}^{-1}x^{f_{j}}g_{j}\cdot H^{\prime }}$.

The cycle decomposition corresponds to a double coset decomposition $G={\dot {\cup }}_{{j=1}}^{t}\,\langle x\rangle g_{j}H$ of the group $G$ modulo the cyclic group $\langle x\rangle$ and modulo the subgroup $H$. It was actually this cycle decomposition form of the transfer homomorphism which was given by E. Artin in his original 1929 paper.^[3]

Transfer to a normal subgroup

Let $H\triangleleft G$ be a normal subgroup of finite index ${\displaystyle n=(G:H)\geq 1}$ in a group $G$. Then we have $xH=Hx$, for all $x\in G$, and there exists the quotient group $G/H$ of order $n$. For an element $x\in G$, we let $f:={\mathrm {ord}}(xH)$ denote the order of the coset $xH$ in $G/H$, and we let ${\displaystyle (\ell _{1},\ldots ,\ell _{t})}$ be a left transversal of the subgroup $\langle x,H\rangle$ in $G$, where $t=n/f$.

Theorem. Then the image of $x\in G$ under the Artin transfer $T_{{G,H}}$ is given by

${\displaystyle (14)\qquad T_{G,H}(x)=\prod _{j=1}^{t}\,g_{j}^{-1}x^{f}g_{j}\cdot H^{\prime }}$.

For the proof click show on the right hand side.

Proof 

$\langle xH\rangle$ is a cyclic subgroup of order $f$ in $G/H$, and a left transversal $(g_{1},\ldots ,g_{t})$ of the subgroup $\langle x,H\rangle$ in $G$,

where $t=n/f$ and $G={\dot {\cup }}_{{j=1}}^{t}\,g_{j}\langle x,H\rangle$ is the corresponding disjoint left coset decomposition,

can be refined to a left transversal ${\displaystyle g_{j}x^{k}}$ ${\displaystyle (1\leq j\leq t,\ 0\leq k\leq f-1)}$ with disjoint left coset decomposition

${\displaystyle (15)\qquad G={\dot {\cup }}_{j=1}^{t}\,{\dot {\cup }}_{k=0}^{f-1}\,g_{j}x^{k}H}$

of $H$ in $G$. Hence, the formula for the image of $x$ under the Artin transfer $T_{{G,H}}$ in the previous section takes the particular shape

$T_{{G,H}}(x)=\prod _{{j=1}}^{t}\,g_{j}^{{-1}}x^{f}g_{j}\cdot H^{\prime }$

with exponent $f$ independent of $j$.

Corollary. In particular, the inner transfer of an element $x\in H$ is given as a symbolic power

${\displaystyle (16)\qquad T_{G,H}(x)=x^{\mathrm {Tr} _{G}(H)}\cdot H^{\prime }}$

with the trace element

${\displaystyle (17)\qquad \mathrm {Tr} _{G}(H)=\sum _{j=1}^{t}\,g_{j}\in \mathbb {Z} \lbrack G\rbrack }$

of $H$ in $G$ as symbolic exponent.

The other extreme is the outer transfer of an element $x\in G\setminus H$ which generates $G$ modulo $H$, that is $G=\langle x,H\rangle$.

It is simply an $n$th power

${\displaystyle (18)\qquad T_{G,H}(x)=x^{n}\cdot H^{\prime }}$.

For the proof click show on the right hand side.

Proof 

The inner transfer of an element $x\in H$, whose coset ${\displaystyle xH=H}$ is the principal set in $G/H$ of order $f=1$, is given as the symbolic power

$T_{{G,H}}(x)=\prod _{{j=1}}^{t}\,g_{j}^{{-1}}xg_{j}\cdot H^{\prime }=\prod _{{j=1}}^{t}\,x^{{g_{j}}}\cdot H^{\prime }=x^{{\sum _{{j=1}}^{t}\,g_{j}}}\cdot H^{\prime }$

with the trace element

${\mathrm {Tr}}_{G}(H)=\sum _{{j=1}}^{t}\,g_{j}\in {\mathbb {Z}}\lbrack G\rbrack$

of $H$ in $G$ as symbolic exponent.

The outer transfer of an element $x\in G\setminus H$ which generates $G$ modulo $H$, that is $G=\langle x,H\rangle$,

whence the coset $xH$ is generator of $G/H$ with order$f=n$, is given as the $n$th power

$T_{{G,H}}(x)=\prod _{{j=1}}^{1}\,1^{{-1}}\cdot x^{n}\cdot 1\cdot H^{\prime }=x^{n}\cdot H^{\prime }$.

Transfers to normal subgroups will be the most important cases in the sequel, since the central concept of this article, the Artin pattern, which endows descendant trees with additional structure, consists of targets and kernels of Artin transfers from a group $G$ to intermediate groups $G^{\prime }\leq H\leq G$ between $G$ and its commutator subgroup $G^{\prime }$. For these intermediate groups we have the following lemma.

Lemma. All subgroups $H\leq G$ of a group $G$ which contain the commutator subgroup $G^{\prime }$ are normal subgroups $H\triangleleft G$.

For the proof click show on the right hand side.

Proof 

Let $G^{\prime }\leq H\leq G$. If $H$ were not a normal subgroup of $G$, then we had ${\displaystyle x^{-1}Hx\not \subseteq H}$ for some element $x\in G\setminus H$. This would imply the existence of elements $h\in H$ and ${\displaystyle y\in G\setminus H}$ such that ${\displaystyle x^{-1}hx=y}$, and consequently the commutator ${\displaystyle \lbrack h,x\rbrack =h^{-1}x^{-1}hx=h^{-1}y}$ would be an element in ${\displaystyle G\setminus H}$ in contradiction to ${\displaystyle G^{\prime }\leq H}$.

Explicit implementations of Artin transfers in the simplest situations are presented in the following section.

Computational implementation

Abelianization of type (p,p)

Let $G$ be a p-group with abelianization $G/G^{\prime }$ of elementary abelian type $(p,p)$. Then $G$ has $p+1$ maximal subgroups $H_{i}<G$ $(1\leq i\leq p+1)$ of index $(G:H_{i})=p$. In this particular case, the Frattini subgroup ${\displaystyle \Phi (G):=\bigcap _{i=1}^{p+1}\,H_{i}}$, which is defined as the intersection of all maximal subgroups, coincides with the commutator subgroup ${\displaystyle G^{\prime }=\lbrack G,G\rbrack }$, since the latter contains all pth powers ${\displaystyle G^{\prime }\geq G^{p}}$, and thus we have ${\displaystyle \Phi (G)=G^{p}\cdot G^{\prime }=G^{\prime }}$.

For each $1\leq i\leq p+1$, let $T_{i}:\,G\to H_{i}/H_{i}^{\prime }$ be the Artin transfer homomorphism from $G$ to the abelianization of $H_{i}$. According to Burnside's basis theorem, the group $G$ has generator rank $d(G)=2$ and can therefore be generated as $G=\langle x,y\rangle$ by two elements $x,y$ such that $x^{p},y^{p}\in G^{\prime }$. For each of the maximal subgroups $H_{i}$, which are normal subgroups $H_{i}\triangleleft G$ by the Lemma in the preceding section, we need a generator $h_{i}$ with respect to $G^{\prime }$, and a generator $t_{i}$ of a transversal ${\displaystyle (1,t_{i},t_{i}^{2},\ldots ,t_{i}^{p-1})}$ such that $H_{i}=\langle h_{i},G^{\prime }\rangle$ and ${\displaystyle G=\langle t_{i},H_{i}\rangle ={\dot {\bigcup }}_{j=0}^{p-1}\,t_{i}^{j}H_{i}}$.

A convenient selection is given by

${\displaystyle (19)\qquad h_{1}=y,\ t_{1}=x,{\text{ and }}h_{i}=xy^{i-2},\ t_{i}=y,{\text{ for all }}2\leq i\leq p+1}$.

Then, for each $1\leq i\leq p+1$, it is possible to implement the inner transfer by

${\displaystyle (20)\qquad T_{i}(h_{i})=h_{i}^{\mathrm {Tr} _{G}(H_{i})}\cdot H_{i}^{\prime }=h_{i}^{1+t_{i}+t_{i}^{2}+\cdots +t_{i}^{p-1}}\cdot H_{i}^{\prime }}$,

according to equation (16) in the last Corollary, which can also be expressed by a product of two pth powers,

${\displaystyle (21)\qquad T_{i}(h_{i})=h_{i}\cdot t_{i}^{-1}h_{i}t_{i}\cdot t_{i}^{-2}h_{i}t_{i}^{2}\cdots t_{i}^{-p+1}h_{i}t_{i}^{p-1}\cdot H_{i}^{\prime }=(h_{i}t_{i}^{-1})^{p}t_{i}^{p}\cdot H_{i}^{\prime }}$,

and to implement the outer transfer as a complete pth power by

${\displaystyle (22)\qquad T_{i}(t_{i})=t_{i}^{p}\cdot H_{i}^{\prime }}$,

according to equation (18) in the preceding Corollary. The reason is that ${\displaystyle \mathrm {ord} (h_{i}H_{i})=1}$ and ${\displaystyle \mathrm {ord} (t_{i}H_{i})=p}$ in the quotient group ${\displaystyle G/H_{i}}$.

It should be pointed out that the complete specification of the Artin transfers $T_{i}$ also requires explicit knowledge of the derived subgroups $H_{i}^{\prime }$. Since $G^{\prime }$ is a normal subgroup of index $p$ in $H_{i}$, a certain general reduction is possible by $H_{i}^{\prime }=\lbrack H_{i},H_{i}\rbrack =\lbrack G^{\prime },H_{i}\rbrack =(G^{\prime })^{{h_{i}-1}}$, ^[10] but a presentation of $G$ must be known for determining generators of $G^{\prime }=\langle s_{1},\ldots ,s_{n}\rangle$, whence

${\displaystyle (23)\qquad H_{i}^{\prime }=(G^{\prime })^{h_{i}-1}=\langle \lbrack s_{1},h_{i}\rbrack ,\ldots ,\lbrack s_{n},h_{i}\rbrack \rangle }$.

Abelianization of type (p²,p)

Let $G$ be a p-group with abelianization $G/G^{\prime }$ of non-elementary abelian type $(p^{2},p)$. Then $G$ has $p+1$ maximal subgroups $H_{i}<G$ $(1\leq i\leq p+1)$ of index $(G:H_{i})=p$ and $p+1$ subgroups $U_{i}<G$ $(1\leq i\leq p+1)$ of index $(G:U_{i})=p^{2}$.

For each $1\leq i\leq p+1$, let $T_{{1,i}}:\,G\to H_{i}/H_{i}^{\prime }$, resp. $T_{{2,i}}:\,G\to U_{i}/U_{i}^{\prime }$, be the Artin transfer homomorphism from $G$ to the abelianization of $H_{i}$, resp. $U_{i}$. Burnside's basis theorem asserts that the group $G$ has generator rank $d(G)=2$ and can therefore be generated as $G=\langle x,y\rangle$ by two elements $x,y$ such that $x^{{p^{2}}},y^{p}\in G^{\prime }$.

We begin by considering the first layer of subgroups. For each of the normal subgroups $H_{i}\triangleleft G$ $(1\leq i\leq p)$, we select a generator

${\displaystyle (24)\qquad h_{i}=xy^{i-1}}$ such that $H_{i}=\langle h_{i},G^{\prime }\rangle$.

These are the cases where the factor group $H_{i}/G^{\prime }$ is cyclic of order $p^{2}$. However, for the distinguished maximal subgroup $H_{{p+1}}$, for which the factor group $H_{{p+1}}/G^{\prime }$ is bicyclic of type $(p,p)$, we need two generators

${\displaystyle (25)\qquad h_{p+1}=y}$ and $h_{0}=x^{p}$ such that $H_{{p+1}}=\langle h_{{p+1}},h_{0},G^{\prime }\rangle$.

Further, a generator $t_{i}$ of a transversal must be given such that $G=\langle t_{i},H_{i}\rangle$, for each $1\leq i\leq p+1$. It is convenient to define

${\displaystyle (26)\qquad t_{i}=y}$, for $1\leq i\leq p$, and $t_{{p+1}}=x$.

Then, for each $1\leq i\leq p+1$, we have the inner transfer

${\displaystyle (27)\qquad T_{1,i}(h_{i})=h_{i}^{\mathrm {Tr} _{G}(H_{i})}\cdot H_{i}^{\prime }=h_{i}^{1+t_{i}+t_{i}^{2}+\ldots +t_{i}^{p-1}}\cdot H_{i}^{\prime }}$,

which equals $(h_{i}t_{i}^{{-1}})^{p}t_{i}^{p}\cdot H_{i}^{\prime }$, and the outer transfer

${\displaystyle (28)\qquad T_{1,i}(t_{i})=t_{i}^{p}\cdot H_{i}^{\prime }}$,

since ${\displaystyle \mathrm {ord} (h_{i}H_{i})=1}$ and ${\displaystyle \mathrm {ord} (t_{i}H_{i})=p}$.

Now we continue by considering the second layer of subgroups. For each of the normal subgroups $U_{i}\triangleleft G$ $(1\leq i\leq p+1)$, we select a generator

${\displaystyle (29)\qquad u_{1}=y}$, $u_{i}=x^{p}y^{{i-1}}$ for $2\leq i\leq p$, and $u_{{p+1}}=x^{p}$,

such that $U_{i}=\langle u_{i},G^{\prime }\rangle$. Among these subgroups, the Frattini subgroup $U_{{p+1}}=\langle x^{p},G^{\prime }\rangle =G^{p}\cdot G^{\prime }$ is particularly distinguished. A uniform way of defining generators $t_{i},w_{i}$ of a transversal such that $G=\langle t_{i},w_{i},U_{i}\rangle$, is to set

${\displaystyle (30)\qquad t_{i}=x,w_{i}=x^{p}}$, for $1\leq i\leq p$, and $t_{{p+1}}=x,w_{{p+1}}=y$.

Since ${\displaystyle \mathrm {ord} (u_{i}U_{i})=1}$, but on the other hand ${\displaystyle \mathrm {ord} (t_{i}U_{i})=p^{2}}$ and ${\displaystyle \mathrm {ord} (w_{i}U_{i})=p}$, for $1\leq i\leq p+1$, with the single exception that ${\displaystyle \mathrm {ord} (t_{p+1}U_{p+1})=p}$, we obtain the following expressions for the inner transfer

${\displaystyle (31)\qquad T_{2,i}(u_{i})=u_{i}^{\mathrm {Tr} _{G}(U_{i})}\cdot U_{i}^{\prime }=u_{i}^{\sum _{j=0}^{p-1}\,\sum _{k=0}^{p-1}\,w_{i}^{j}t_{i}^{k}}\cdot U_{i}^{\prime }=\prod _{j=0}^{p-1}\,\prod _{k=0}^{p-1}\,(w_{i}^{j}t_{i}^{k})^{-1}u_{i}w_{i}^{j}t_{i}^{k}\cdot U_{i}^{\prime }}$,

and for the outer transfer

${\displaystyle (32)\qquad T_{2,i}(t_{i})=t_{i}^{p^{2}}\cdot U_{i}^{\prime }}$,

exceptionally

${\displaystyle (33)\qquad T_{2,p+1}(t_{p+1})=(t_{p+1}^{p})^{1+w_{p+1}+w_{p+1}^{2}+\ldots +w_{p+1}^{p-1}}\cdot U_{p+1}^{\prime }}$,

and

${\displaystyle (34)\qquad T_{2,i}(w_{i})=(w_{i}^{p})^{1+t_{i}+t_{i}^{2}+\ldots +t_{i}^{p-1}}\cdot U_{i}^{\prime }}$,

for $1\leq i\leq p+1$. Again, it should be emphasized that the structure of the derived subgroups $H_{i}^{\prime }$ and $U_{i}^{\prime }$ must be known to specify the action of the Artin transfers completely.

Transfer kernels and targets

Let $G$ be a group with finite abelianization $G/G^{\prime }$. Suppose that $(H_{i})_{{i\in I}}$ denotes the family of all subgroups $H_{i}\triangleleft G$ which contain the commutator subgroup $G^{\prime }$ and are therefore necessarily normal, enumerated by means of the finite index set $I$. For each $i\in I$, let $T_{i}:=T_{{G,H_{i}}}$ be the Artin transfer from $G$ to the abelianization $H_{i}/H_{i}^{\prime }$.

Definition. ^[11]

The family of normal subgroups $\varkappa _{H}(G)=(\ker(T_{i}))_{{i\in I}}$ is called the transfer kernel type (TKT) of $G$ with respect to $(H_{i})_{{i\in I}}$, and the family of abelianizations (resp. their abelian type invariants) $\tau _{H}(G)=(H_{i}/H_{i}^{\prime })_{{i\in I}}$ is called the transfer target type (TTT) of $G$ with respect to $(H_{i})_{{i\in I}}$. Both families are also called multiplets whereas a single component will be referred to as a singulet.

Important examples for these concepts are provided in the following two sections.

Abelianization of type (p,p)

Let $G$ be a p-group with abelianization $G/G^{\prime }$ of elementary abelian type $(p,p)$. Then $G$ has $p+1$ maximal subgroups $H_{i}<G$ $(1\leq i\leq p+1)$ of index $(G:H_{i})=p$. For each $1\leq i\leq p+1$, let $T_{i}:\,G\to H_{i}/H_{i}^{\prime }$ be the Artin transfer homomorphism from $G$ to the abelianization of $H_{i}$.

Definition.

The family of normal subgroups $\varkappa _{H}(G)=(\ker(T_{i}))_{{1\leq i\leq p+1}}$ is called the transfer kernel type (TKT) of $G$ with respect to $H_{1},\ldots ,H_{{p+1}}$.

Remarks.

• For brevity, the TKT is identified with the multiplet $(\varkappa (i))_{{1\leq i\leq p+1}}$, whose integer components are given by $\varkappa (i)={\begin{cases}0&{\text{if }}\ker(T_{i})=G,\\j&{\text{if }}\ker(T_{i})=H_{j}{\text{ for some }}1\leq j\leq p+1.\end{cases}}$ Here, we take into consideration that each transfer kernel $\ker(T_{i})$ must contain the commutator subgroup $G^{\prime }$ of $G$, since the transfer target $H_{i}/H_{i}^{\prime }$ is abelian. However, the minimal case $\ker(T_{i})=G^{\prime }$ cannot occur.
• A renumeration of the maximal subgroups $K_{i}=H_{{\pi (i)}}$ and of the transfers $V_{i}=T_{{\pi (i)}}$ by means of a permutation $\pi \in S_{{p+1}}$ gives rise to a new TKT $\lambda _{K}(G)=(\ker(V_{i}))_{{1\leq i\leq p+1}}$ with respect to $K_{1},\ldots ,K_{{p+1}}$, identified with $(\lambda (i))_{{1\leq i\leq p+1}}$, where $\lambda (i)={\begin{cases}0&{\text{ if }}\ker(V_{i})=G,\\j&{\text{ if }}\ker(V_{i})=K_{j}{\text{ for some }}1\leq j\leq p+1.\end{cases}}$ It is adequate to view the TKTs $\lambda _{K}(G)\sim \varkappa _{H}(G)$ as equivalent. Since we have $K_{{\lambda (i)}}=\ker(V_{i})=\ker(T_{{\pi (i)}})=H_{{\varkappa (\pi (i))}}=K_{{{\tilde {\pi }}^{{-1}}(\varkappa (\pi (i)))}}$, the relation between $\lambda$ and $\varkappa$ is given by $\lambda ={\tilde {\pi }}^{{-1}}\circ \varkappa \circ \pi$. Therefore, $\lambda$ is another representative of the orbit $\varkappa ^{{S_{{p+1}}}}$ of $\varkappa$ under the operation $(\pi ,\mu )\mapsto {\tilde {\pi }}^{{-1}}\circ \mu \circ \pi$ of the symmetric group $S_{{p+1}}$ on the set of all mappings from $\lbrace 1,\ldots ,p+1\rbrace$ to $\lbrace 0,\ldots ,p+1\rbrace$, where the extension ${\tilde {\pi }}\in S_{{p+2}}$ of the permutation $\pi \in S_{{p+1}}$ is defined by ${\tilde {\pi }}(0)=0$, and formally $H_{0}=G$, $K_{0}=G$.

Definition.

The orbit $\varkappa (G)=\varkappa ^{{S_{{p+1}}}}$ of any representative $\varkappa$ is an invariant of the p-group $G$ and is called its transfer kernel type, briefly TKT.

Remark.

Let $\#{\mathcal {H}}_{0}(G):=\#\lbrace 1\leq i\leq p+1\mid \varkappa (i)=0\rbrace$ denote the counter of total transfer kernels $\ker(T_{i})=G$, which is an invariant of the group $G$. In 1980, S. M. Chang and R. Foote ^[12] proved that, for any odd prime $p$ and for any integer $0\leq n\leq p+1$, there exist metabelian p-groups $G$ having abelianization $G/G^{\prime }$ of type $(p,p)$ such that $\#{\mathcal {H}}_{0}(G)=n$. However, for $p=2$, there do not exist non-abelian $2$-groups $G$ with $G/G^{\prime }\simeq (2,2)$, which must be metabelian of maximal class, such that $\#{\mathcal {H}}_{0}(G)\geq 2$. Only the elementary abelian $2$-group $G=C_{2}\times C_{2}$ has $\#{\mathcal {H}}_{0}(G)=3$. See Figure 5.

In the following concrete examples for the counters $\#{\mathcal {H}}_{0}(G)$, and also in the remainder of this article, we use identifiers of finite p-groups in the SmallGroups Library by H. U. Besche, B. Eick and E. A. O'Brien .^{[13] [14]}

For $p=3$, we have

• $\#{\mathcal {H}}_{0}(G)=0$ for the extra special group $G=\langle 27,4\rangle$ of exponent $9$ with TKT $\varkappa =(1111)$ (Figure 6),
• $\#{\mathcal {H}}_{0}(G)=1$ for the two groups $G\in \lbrace \langle 243,6\rangle ,\langle 243,8\rangle \rbrace$ with TKTs $\varkappa \in \lbrace (0122),(2034)\rbrace$ (Figures 8 and 9),
• $\#{\mathcal {H}}_{0}(G)=2$ for the group $G=\langle 243,3\rangle$ with TKT $\varkappa =(0043)$ (Figure 4 in the article on descendant trees),
• $\#{\mathcal {H}}_{0}(G)=3$ for the group $G=\langle 81,7\rangle$ with TKT $\varkappa =(2000)$ (Figure 6),
• $\#{\mathcal {H}}_{0}(G)=4$ for the extra special group $G=\langle 27,3\rangle$ of exponent $3$ with TKT $\varkappa =(0000)$ (Figure 6).

Abelianization of type (p²,p)

Let $G$ be a p-group with abelianization $G/G^{\prime }$ of non-elementary abelian type $(p^{2},p)$. Then $G$ possesses $p+1$ maximal subgroups $H_{i}<G$ $(1\leq i\leq p+1)$ of index $(G:H_{i})=p$, and $p+1$ subgroups $U_{i}<G$ $(1\leq i\leq p+1)$ of index $(G:U_{i})=p^{2}$.

Assumption.

Suppose that $H_{{p+1}}=\prod _{{j=1}}^{{p+1}}\,U_{j}$ is the distinguished maximal subgroup which is the product of all subgroups of index $p^{2}$, and $U_{{p+1}}=\cap _{{j=1}}^{{p+1}}\,H_{j}$ is the distinguished subgroup of index $p^{2}$ which is the intersection of all maximal subgroups, that is the Frattini subgroup $\Phi (G)$ of $G$.

First layer

For each $1\leq i\leq p+1$, let $T_{{1,i}}:\,G\to H_{i}/H_{i}^{\prime }$ be the Artin transfer homomorphism from $G$ to the abelianization of $H_{i}$.

Definition.

The family $\varkappa _{{1,H,U}}(G)=(\ker(T_{{1,i}}))_{{1\leq i\leq p+1}}$ is called the first layer transfer kernel type of $G$ with respect to $H_{1},\ldots ,H_{{p+1}}$ and $U_{1},\ldots ,U_{{p+1}}$, and is identified with $(\varkappa _{1}(i))_{{1\leq i\leq p+1}}$, where $\varkappa _{1}(i)={\begin{cases}0&{\text{ if }}\ker(T_{{1,i}})=H_{{p+1}},\\j&{\text{ if }}\ker(T_{{1,i}})=U_{j}{\text{ for some }}1\leq j\leq p+1.\end{cases}}$

Remark.

Here, we observe that each first layer transfer kernel is of exponent $p$ with respect to $G^{\prime }$ and consequently cannot coincide with $H_{j}$ for any $1\leq j\leq p$, since $H_{j}/G^{\prime }$ is cyclic of order $p^{2}$, whereas $H_{{p+1}}/G^{\prime }$ is bicyclic of type $(p,p)$.

Second layer

For each $1\leq i\leq p+1$, let $T_{{2,i}}:\,G\to U_{i}/U_{i}^{\prime }$ be the Artin transfer homomorphism from $G$ to the abelianization of $U_{i}$.

Definition.

The family $\varkappa _{{2,U,H}}(G)=(\ker(T_{{2,i}}))_{{1\leq i\leq p+1}}$ is called the second layer transfer kernel type of $G$ with respect to $U_{1},\ldots ,U_{{p+1}}$ and $H_{1},\ldots ,H_{{p+1}}$, and is identified with $(\varkappa _{2}(i))_{{1\leq i\leq p+1}}$, where $\varkappa _{2}(i)={\begin{cases}0&{\text{ if }}\ker(T_{{2,i}})=G,\\j&{\text{ if }}\ker(T_{{2,i}})=H_{j}{\text{ for some }}1\leq j\leq p+1.\end{cases}}$

Transfer kernel type

Combining the information on the two layers, we obtain the (complete) transfer kernel type $\varkappa _{{H,U}}(G)=(\varkappa _{{1,H,U}}(G);\varkappa _{{2,U,H}}(G))$ of the p-group $G$ with respect to $H_{1},\ldots ,H_{{p+1}}$ and $U_{1},\ldots ,U_{{p+1}}$.

Remark.

The distinguished subgroups $H_{{p+1}}$ and $U_{{p+1}}=\Phi (G)$ are unique invariants of $G$ and should not be renumerated. However, independent renumerations of the remaining maximal subgroups $K_{i}=H_{{\tau (i)}}$ $(1\leq i\leq p)$ and the transfers $V_{{1,i}}=T_{{1,\tau (i)}}$ by means of a permutation $\tau \in S_{p}$, and of the remaining subgroups $W_{i}=U_{{\sigma (i)}}$ $(1\leq i\leq p)$ of index $p^{2}$ and the transfers $V_{{2,i}}=T_{{2,\sigma (i)}}$ by means of a permutation $\sigma \in S_{p}$, give rise to new TKTs $\lambda _{{1,K,W}}(G)=(\ker(V_{{1,i}}))_{{1\leq i\leq p+1}}$ with respect to $K_{1},\ldots ,K_{{p+1}}$ and $W_{1},\ldots ,W_{{p+1}}$, identified with $(\lambda _{1}(i))_{{1\leq i\leq p+1}}$, where $\lambda _{1}(i)={\begin{cases}0&{\text{ if }}\ker(V_{{1,i}})=K_{{p+1}},\\j&{\text{ if }}\ker(V_{{1,i}})=W_{j}{\text{ for some }}1\leq j\leq p+1,\end{cases}}$ and $\lambda _{{2,W,K}}(G)=(\ker(V_{{2,i}}))_{{1\leq i\leq p+1}}$ with respect to $W_{1},\ldots ,W_{{p+1}}$ and $K_{1},\ldots ,K_{{p+1}}$, identified with $(\lambda _{2}(i))_{{1\leq i\leq p+1}}$, where $\lambda _{2}(i)={\begin{cases}0&{\text{ if }}\ker(V_{{2,i}})=G,\\j&{\text{ if }}\ker(V_{{2,i}})=K_{j}{\text{ for some }}1\leq j\leq p+1.\end{cases}}$ It is adequate to view the TKTs $\lambda _{{1,K,W}}(G)\sim \varkappa _{{1,H,U}}(G)$ and $\lambda _{{2,W,K}}(G)\sim \varkappa _{{2,U,H}}(G)$ as equivalent. Since we have $W_{{\lambda _{1}(i)}}=\ker(V_{{1,i}})=\ker(T_{{1,{\hat {\tau }}(i)}})=U_{{\varkappa _{1}({\hat {\tau }}(i))}}=W_{{{\tilde {\sigma }}^{{-1}}(\varkappa _{1}({\hat {\tau }}(i)))}}$, resp. $K_{{\lambda _{2}(i)}}=\ker(V_{{2,i}})=\ker(T_{{2,{\hat {\sigma }}(i)}})=H_{{\varkappa _{2}({\hat {\sigma }}(i))}}=K_{{{\tilde {\tau }}^{{-1}}(\varkappa _{2}({\hat {\sigma }}(i)))}}$, the relations between $\lambda _{1}$ and $\varkappa _{1}$, resp. $\lambda _{2}$ and $\varkappa _{2}$, are given by $\lambda _{1}={\tilde {\sigma }}^{{-1}}\circ \varkappa _{1}\circ {\hat {\tau }}$, resp. $\lambda _{2}={\tilde {\tau }}^{{-1}}\circ \varkappa _{2}\circ {\hat {\sigma }}$. Therefore, $\lambda =(\lambda _{1},\lambda _{2})$ is another representative of the orbit $\varkappa ^{{S_{p}\times S_{p}}}$ of $\varkappa =(\varkappa _{1},\varkappa _{2})$ under the operation $((\sigma ,\tau ),(\mu _{1},\mu _{2}))\mapsto ({\tilde {\sigma }}^{{-1}}\circ \mu _{1}\circ {\hat \tau },{\tilde {\tau }}^{{-1}}\circ \mu _{2}\circ {\hat \sigma })$ of the product of two symmetric groups $S_{p}\times S_{p}$ on the set of all pairs of mappings from $\lbrace 1,\ldots ,p+1\rbrace$ to $\lbrace 0,\ldots ,p+1\rbrace$, where the extensions ${\hat {\pi }}\in S_{{p+1}}$ and ${\tilde {\pi }}\in S_{{p+2}}$ of a permutation $\pi \in S_{p}$ are defined by ${\hat {\pi }}(p+1)={\tilde {\pi }}(p+1)=p+1$ and ${\tilde {\pi }}(0)=0$, and formally $H_{0}=K_{0}=G$, $K_{{p+1}}=H_{{p+1}}$, $U_{0}=W_{0}=H_{{p+1}}$, and $W_{{p+1}}=U_{{p+1}}=\Phi (G)$.

Definition.

The orbit $\varkappa (G)=\varkappa ^{{S_{p}\times S_{p}}}$ of any representative $\varkappa =(\varkappa _{1},\varkappa _{2})$ is an invariant of the p-group $G$ and is called its transfer kernel type, briefly TKT.

Connections between layers

The Artin transfer $T_{{2,i}}:\,G\to U_{i}/U_{i}^{\prime }$ from $G$ to a subgroup $U_{i}$ of index $(G:U_{i})=p^{2}$ ($1\leq i\leq p+1$) is the compositum $T_{{2,i}}={\tilde {T}}_{{H_{j},U_{i}}}\circ T_{{1,j}}$ of the induced transfer ${\tilde {T}}_{{H_{j},U_{i}}}:\,H_{j}/H_{j}^{\prime }\to U_{i}/U_{i}^{\prime }$ from $H_{j}$ to $U_{i}$ and the Artin transfer $T_{{1,j}}:\,G\to H_{j}/H_{j}^{\prime }$ from $G$ to $H_{j}$, for any intermediate subgroup $U_{i}<H_{j}<G$ of index $(G:H_{j})=p$ ($1\leq j\leq p+1$). There occur two situations:

• For the subgroups $U_{1},\ldots ,U_{p}$ only the distinguished maximal subgroup $H_{{p+1}}$ is an intermediate subgroup.
• For the Frattini subgroup $U_{{p+1}}=\Phi (G)$ all maximal subgroups $H_{1},\ldots ,H_{{p+1}}$ are intermediate subgroups.

This causes restrictions for the transfer kernel type $\varkappa _{2}(G)$ of the second layer, since $\ker(T_{{2,i}})=\ker({\tilde {T}}_{{H_{j},U_{i}}}\circ T_{{1,j}})\supset \ker(T_{{1,j}})$, and thus

• $\ker(T_{{2,i}})\supset \ker(T_{{1,p+1}})$, for all $1\leq i\leq p$,
• but even $\ker(T_{{2,p+1}})\supset \langle \cup _{{j=1}}^{{p+1}}\,\ker(T_{{1,j}})\rangle$.

Furthermore, when $G=\langle x,y\rangle$ with $x^{p}\notin G^{\prime }$ and $y^{p}\in G^{\prime }$, an element $xy^{{k-1}}$ ($1\leq k\leq p$) which is of order $p^{2}$ with respect to $G^{\prime }$, can belong to the transfer kernel $\ker(T_{{2,i}})$ only if its $p$th power $x^{p}$ is contained in $\ker(T_{{1,j}})$, for all intermediate subgroups $U_{i}<H_{j}<G$, and thus:

• $xy^{{k-1}}\in \ker(T_{{2,i}})$, for certain $1\leq i,k\leq p$, enforces the first layer TKT singulet $\varkappa _{1}(p+1)=p+1$,
• but $xy^{{k-1}}\in \ker(T_{{2,p+1}})$, for some $1\leq k\leq p$, even specifies the complete first layer TKT multiplet $\varkappa _{1}=((p+1)^{{p+1}})$, that is $\varkappa _{1}(j)=p+1$, for all $1\leq j\leq p+1$.

Figure 1: Factoring through the abelianization.

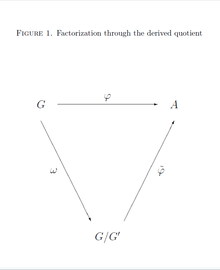
Inheritance from quotients

The common feature of all parent-descendant relations between finite p-groups is that the parent $\pi (G)$ is a quotient $G/N$ of the descendant $G$ by a suitable normal subgroup $N\triangleleft G$. Thus, an equivalent definition can be given by selecting an epimorphism $\varphi$ from $G$ onto a group ${\tilde {G}}$ whose kernel $\ker(\varphi )$ plays the role of the normal subgroup $N\triangleleft G$. Then the group ${\tilde {G}}=\varphi (G)$ can be viewed as the parent of the descendant $G$. In the following sections, this point of view will be taken, generally for arbitrary groups, not only for finite p-groups.

Passing through the abelianization

If $\varphi :\ G\to A$ is a homomorphism from a group $G$ to an abelian group $A$, then there exists a unique homomorphism ${\tilde {\varphi }}:\ G/G^{\prime }\to A$ such that $\varphi ={\tilde {\varphi }}\circ \omega$, where $\omega :\ G\to G/G^{\prime }$ denotes the canonical projection onto the abelianization $G/G^{\prime }$ of $G$. The kernel of ${\tilde {\varphi }}$ is given by $\ker({\tilde {\varphi }})=\ker(\varphi )/G^{\prime }$. The situation is visualized in Figure 1.

This statement is a consequence of the second Corollary in the article on the induced homomorphism. Nevertheless, we give an independent proof for the present situation.

Proof. The uniqueness of ${\tilde {\varphi }}$ is a consequence of the condition $\varphi ={\tilde {\varphi }}\circ \omega$, which implies that ${\tilde {\varphi }}$ must be defined by ${\tilde {\varphi }}(xG^{\prime })={\tilde {\varphi }}(\omega (x))=({\tilde {\varphi }}\circ \omega )(x)=\varphi (x)$, for any $x\in G$.

The relation ${\tilde {\varphi }}(xG^{\prime }\cdot yG^{\prime })={\tilde {\varphi }}((xy)G^{\prime })=\varphi (xy)=\varphi (x)\cdot \varphi (y)={\tilde {\varphi }}(xG^{\prime })\cdot {\tilde {\varphi }}(xG^{\prime })$, for $x,y\in G$, shows that ${\tilde {\varphi }}$ is a homomorphism.

For the commutator of $x,y\in G$, we have ${\displaystyle \varphi (\lbrack x,y\rbrack )=\varphi (x^{-1}y^{-1}xy)=\varphi (x^{-1})\varphi (y^{-1})\varphi (x)\varphi (y)=\lbrack \varphi (x),\varphi (y)\rbrack =1}$, since $A$ is abelian. Thus, the commutator subgroup $G^{\prime }$ of $G$ is contained in the kernel $\ker(\varphi )$, and this finally shows that the definition of ${\tilde {\varphi }}$ is independent of the coset representative, $xG^{\prime }=yG^{\prime }$ $\Rightarrow$ ${\displaystyle y^{-1}x\in G^{\prime }\leq \ker(\varphi )}$ $\Rightarrow$ ${\displaystyle {\tilde {\varphi }}(yG^{\prime })^{-1}\cdot {\tilde {\varphi }}(xG^{\prime })={\tilde {\varphi }}(y^{-1}xG^{\prime })=\varphi (y^{-1}x)=1}$ $\Rightarrow$ ${\tilde {\varphi }}(xG^{\prime })={\tilde {\varphi }}(yG^{\prime })$.

Figure 2: Epimorphisms and derived quotients.

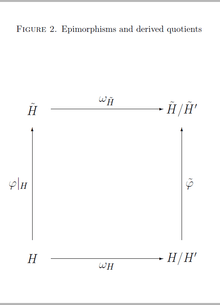
TTT singulets

Let $G$ and ${\tilde {G}}$ be groups such that ${\tilde {G}}=\varphi (G)$ is the image of $G$ under an epimorphism $\varphi :\ G\to {\tilde {G}}$ and ${\tilde {H}}=\varphi (H)$ is the image of a subgroup $H\leq G$.

The commutator subgroup of ${\tilde {H}}$ is the image of the commutator subgroup of $H$, that is ${\tilde {H}}^{\prime }=\varphi (H^{\prime })$. Therefore, $\varphi$ induces a unique epimorphism ${\tilde {\varphi }}:\ H/H^{\prime }\to {\tilde {H}}/{\tilde {H}}^{\prime }$, and thus ${\tilde {H}}/{\tilde {H}}^{\prime }$ is an epimorphic image of $H/H^{\prime }$, or with other words, a quotient of $H/H^{\prime }$.

Moreover, if $\ker(\varphi )\leq H^{\prime }$, then the map ${\tilde {\varphi }}$ is an isomorphism, and the abelianizations ${\tilde {H}}/{\tilde {H}}^{\prime }\simeq H/H^{\prime }$ are isomorphic. See Figure 2 for a visualization of this scenario.

This claim is a consequence of the Main Theorem in the article on the induced homomorphism. Nevertheless, an independent proof is given as follows.

Proof. The statements can be seen in the following manner.

Firstly, the image of the commutator subgroup is $\varphi (H^{\prime })=\varphi (\lbrack H,H\rbrack )=\varphi (\langle \lbrack u,v\rbrack \mid u,v\in H\rangle )$ $=\langle \lbrack \varphi (u),\varphi (v)\rbrack \mid u,v\in H\rangle =\lbrack \varphi (H),\varphi (H)\rbrack =\varphi (H)^{\prime }={\tilde {H}}^{\prime }$.

Secondly, the epimorphism $\varphi$ can be restricted to an epimorphism $\varphi \vert _{H}:\ H\to {\tilde {H}}$. According to the previous section, the composite epimorphism $(\omega _{{{\tilde {H}}}}\circ \varphi \vert _{H}):\ H\to {\tilde {H}}/{\tilde {H}}^{\prime }$ from $H$ onto the abelian group ${\tilde {H}}/{\tilde {H}}^{\prime }$ factors through $H/H^{\prime }$ by means of a uniquely determined epimorphism ${\tilde {\varphi }}:\ H/H^{\prime }\to {\tilde {H}}/{\tilde {H}}^{\prime }$ such that ${\tilde {\varphi }}\circ \omega _{H}=\omega _{{{\tilde {H}}}}\circ \varphi \vert _{H}$.

Consequently, we have ${\tilde {H}}/{\tilde {H}}^{\prime }\simeq (H/H^{\prime })/\ker({\tilde {\varphi }})$.

Furthermore, the kernel of ${\tilde {\varphi }}$ is given explicitly by ${\displaystyle \ker({\tilde {\varphi }})=(H^{\prime }\cdot \ker(\varphi ))/H^{\prime }}$.

Finally, if $\ker(\varphi )\leq H^{\prime }$, then ${\tilde {\varphi }}$ is an isomorphism, since $\ker({\tilde {\varphi }})=H^{\prime }/H^{\prime }=1$.

Definition. ^[15]

Due to the results in the present section, it makes sense to define a partial order on the set of abelian type invariants by putting ${\tilde {H}}/{\tilde {H}}^{\prime }\preceq H/H^{\prime }$, when ${\tilde {H}}/{\tilde {H}}^{\prime }\simeq (H/H^{\prime })/\ker({\tilde {\varphi }})$, and ${\tilde {H}}/{\tilde {H}}^{\prime }=H/H^{\prime }$, when ${\tilde {H}}/{\tilde {H}}^{\prime }\simeq H/H^{\prime }$.

Figure 3: Epimorphisms and Artin transfers.

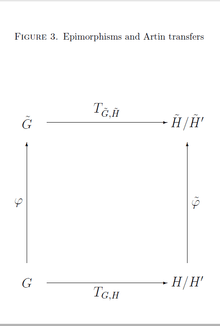
TKT singulets

Suppose that $G$ and ${\tilde {G}}$ are groups, ${\tilde {G}}=\varphi (G)$ is the image of $G$ under an epimorphism $\varphi :\ G\to {\tilde {G}}$, and ${\tilde {H}}=\varphi (H)$ is the image of a subgroup $H\leq G$ of finite index $n=(G:H)$. Let $T_{{G,H}}$ be the Artin transfer from $G$ to $H/H^{\prime }$ and $T_{{{\tilde {G}},{\tilde {H}}}}$ be the Artin transfer from ${\tilde {G}}$ to ${\tilde {H}}/{\tilde {H}}^{\prime }$.

If $\ker(\varphi )\leq H$, then the image $(\varphi (g_{1}),\ldots ,\varphi (g_{n}))$ of a left transversal $(g_{1},\ldots ,g_{n})$ of $H$ in $G$ is a left transversal of ${\tilde {H}}$ in ${\tilde {G}}$, and the inclusion $\varphi (\ker(T_{{G,H}}))\leq \ker(T_{{{\tilde {G}},{\tilde {H}}}})$ holds.

Moreover, if even $\ker(\varphi )\leq H^{\prime }$, then the equation $\varphi (\ker(T_{{G,H}}))=\ker(T_{{{\tilde {G}},{\tilde {H}}}})$ holds. See Figure 3 for a visualization of this scenario.

Proof. The truth of these statements can be justified in the following way.

Let $(g_{1},\ldots ,g_{n})$ be a left transversal of $H$ in $G$. Then $G={\dot {\cup }}_{{i=1}}^{n}\,g_{i}H$ is a disjoint union but $\varphi (G)={\dot {\cup }}_{{i=1}}^{n}\,\varphi (g_{i})\varphi (H)$ is not necessarily disjoint. For $1\leq j,k\leq n$, we have $\varphi (g_{j})\varphi (H)=\varphi (g_{k})\varphi (H)$$\Leftrightarrow$ $\varphi (H)=\varphi (g_{j})^{{-1}}\varphi (g_{k})\varphi (H)=\varphi (g_{j}^{{-1}}g_{k})\varphi (H)$ $\Leftrightarrow$ $\varphi (g_{j}^{{-1}}g_{k})=\varphi (h)$ for some element $h\in H$ $\Leftrightarrow$ $\varphi (h^{{-1}}g_{j}^{{-1}}g_{k})=1$ $\Leftrightarrow$ $h^{{-1}}g_{j}^{{-1}}g_{k}=:k\in \ker(\varphi )$. However, if the condition $\ker(\varphi )\leq H$ is satisfied, then we are able to conclude that $g_{j}^{{-1}}g_{k}=hk\in H$, and thus $j=k$.

This has been shown already in the Proposition of the initial section on transversals of a subgroup.

Let ${\tilde {\varphi }}:\ H/H^{\prime }\to {\tilde {H}}/{\tilde {H}}^{\prime }$ be the epimorphism obtained in the manner indicated in the previous section. For the image of $x\in G$ under the Artin transfer, we have ${\displaystyle {\tilde {\varphi }}(T_{G,H}(x))={\tilde {\varphi }}(\prod _{i=1}^{n}\,g_{\pi _{x}(i)}^{-1}xg_{i}\cdot H^{\prime })=\prod _{i=1}^{n}\,\varphi (g_{\pi _{x}(i)})^{-1}\varphi (x)\varphi (g_{i})\cdot \varphi (H^{\prime })}$. Since $\varphi (H^{\prime })=\varphi (H)^{\prime }={\tilde {H}}^{\prime }$, the right hand side equals $T_{{{\tilde {G}},{\tilde {H}}}}(\varphi (x))$, provided that $(\varphi (g_{1}),\ldots ,\varphi (g_{n}))$ is a left transversal of ${\tilde {H}}$ in ${\tilde {G}}$, which is correct, when $\ker(\varphi )\leq H$. This shows that the diagram in Figure 3 is commutative, that is ${\tilde {\varphi }}\circ T_{{G,H}}=T_{{{\tilde {G}},{\tilde {H}}}}\circ \varphi$. Consequently, we obtain the inclusion $\varphi (\ker(T_{{G,H}}))\leq \ker(T_{{{\tilde {G}},{\tilde {H}}}})$, if $\ker(\varphi )\leq H$. Finally, if $\ker(\varphi )\leq H^{\prime }$, then the previous section has shown that ${\tilde {\varphi }}$ is an isomorphism. Using the inverse isomorphism, we get $T_{{G,H}}={\tilde {\varphi }}^{{-1}}\circ T_{{{\tilde {G}},{\tilde {H}}}}\circ \varphi$, which proves ${\displaystyle \varphi ^{-1}(\ker(T_{{\tilde {G}},{\tilde {H}}}))\leq \ker(T_{G,H})}$, ${\displaystyle \ker(T_{{\tilde {G}},{\tilde {H}}})=\varphi (\varphi ^{-1}(\ker(T_{{\tilde {G}},{\tilde {H}}})))\leq \varphi (\ker(T_{G,H}))}$, and thus the equation $\varphi (\ker(T_{{G,H}}))=\ker(T_{{{\tilde {G}},{\tilde {H}}}})$.

Definition. ^[15]

In view of the results in the present section, we are able to define a partial order of transfer kernels by setting $\ker(T_{{G,H}})\preceq \ker(T_{{{\tilde {G}},{\tilde {H}}}})$, when $\varphi (\ker(T_{{G,H}}))\leq \ker(T_{{{\tilde {G}},{\tilde {H}}}})$, and $\ker(T_{{G,H}})=\ker(T_{{{\tilde {G}},{\tilde {H}}}})$, when $\varphi (\ker(T_{{G,H}}))=\ker(T_{{{\tilde {G}},{\tilde {H}}}})$.

TTT and TKT multiplets

Suppose $G$ and ${\tilde {G}}$ are groups, ${\tilde {G}}=\varphi (G)$ is the image of $G$ under an epimorphism $\varphi :\ G\to {\tilde {G}}$, and both groups have isomorphic finite abelianizations $G/G^{\prime }\simeq {\tilde {G}}/{\tilde {G}}^{\prime }$. Let $(H_{i})_{{i\in I}}$ denote the family of all subgroups $H_{i}\triangleleft G$ which contain the commutator subgroup $G^{\prime }$ (and thus are necessarily normal), enumerated by means of the finite index set $I$, and let ${\tilde {H_{i}}}=\varphi (H_{i})$ be the image of $H_{i}$ under $\varphi$, for each $i\in I$. Assume that, for each $i\in I$, $T_{i}:=T_{{G,H_{i}}}$ denotes the Artin transfer from $G$ to the abelianization $H_{i}/H_{i}^{\prime }$, and ${\tilde {T}}_{i}:=T_{{{\tilde {G}},{\tilde {H}}_{i}}}$ denotes the Artin transfer from ${\tilde {G}}$ to the abelianization ${\tilde {H}}_{i}/{\tilde {H}}_{i}^{\prime }$. Finally, let $J\subseteq I$ be any non-empty subset of $I$.

Then it is convenient to define $\varkappa _{H}(G)=(\ker(T_{j}))_{{j\in J}}$, called the (partial) transfer kernel type (TKT) of $G$ with respect to $(H_{j})_{{j\in J}}$, and $\tau _{H}(G)=(H_{j}/H_{j}^{\prime })_{{j\in J}}$, called the (partial) transfer target type (TTT) of $G$ with respect to $(H_{j})_{{j\in J}}$.

Due to the rules for singulets, established in the preceding two sections, these multiplets of TTTs and TKTs obey the following fundamental inheritance laws:

1. If $\ker(\varphi )\leq \cap _{{j\in J}}\,H_{j}$, then $\tau _{{{\tilde {H}}}}({\tilde {G}})\preceq \tau _{H}(G)$, in the sense that ${\tilde {H}}_{j}/{\tilde {H}}_{j}^{\prime }\preceq H_{j}/H_{j}^{\prime }$, for each $j\in J$, and $\varkappa _{H}(G)\preceq \varkappa _{{{\tilde {H}}}}({\tilde {G}})$, in the sense that $\ker(T_{j})\preceq \ker({\tilde {T}}_{j})$, for each $j\in J$.
2. If $\ker(\varphi )\leq \cap _{{j\in J}}\,H_{j}^{\prime }$, then $\tau _{{{\tilde {H}}}}({\tilde {G}})=\tau _{H}(G)$, in the sense that ${\tilde {H}}_{j}/{\tilde {H}}_{j}^{\prime }=H_{j}/H_{j}^{\prime }$, for each $j\in J$, and $\varkappa _{H}(G)=\varkappa _{{{\tilde {H}}}}({\tilde {G}})$, in the sense that $\ker(T_{j})=\ker({\tilde {T}}_{j})$, for each $j\in J$.

Inherited automorphisms

A further inheritance property does not immediately concern Artin transfers but will prove to be useful in applications to descendant trees.

Let $G$ and ${\tilde {G}}$ be groups such that ${\tilde {G}}=\varphi (G)\simeq G/\ker(\varphi )$ is the image of $G$ under an epimorphism $\varphi :\ G\to {\tilde {G}}$. Suppose that $\sigma \in {\mathrm {Aut}}(G)$ is an automorphism of $G$.

If $\sigma (\ker(\varphi ))\leq \ker(\varphi )$, then there exists a unique epimorphism ${\tilde {\sigma }}:\,{\tilde {G}}\to {\tilde {G}}$ such that $\varphi \circ \sigma ={\tilde {\sigma }}\circ \varphi$. If $\sigma (\ker(\varphi ))=\ker(\varphi )$, then ${\tilde {\sigma }}\in {\mathrm {Aut}}({\tilde {G}})$ is also an automorphism.

The justification for these facts is based on the isomorphic representation ${\tilde {G}}=\varphi (G)\simeq G/\ker(\varphi )$, which permits to identify ${\tilde {\sigma }}(g\ker(\varphi )){\hat {=}}{\tilde {\sigma }}(\varphi (g))=\varphi (\sigma (g)){\hat {=}}\sigma (g)\ker(\varphi )$ for all $g\in G$ and proves the uniqueness of ${\tilde {\sigma }}$. If $\sigma (\ker(\varphi ))\leq \ker(\varphi )$, then the consistency follows from $g\ker(\varphi )=h\ker(\varphi )$ $\Rightarrow$ $h^{{-1}}g\in \ker(\varphi )$ $\Rightarrow$ $\sigma (h^{{-1}}g)\in \ker(\varphi )$ $\Rightarrow$ $\sigma (g)\ker(\varphi )=\sigma (h)\ker(\varphi )$. And if $\sigma (\ker(\varphi ))=\ker(\varphi )$, then injectivity of ${\tilde {\sigma }}$ is a consequence of ${\tilde {\sigma }}(g\ker(\varphi )){\hat {=}}\sigma (g)\ker(\varphi )=\ker(\varphi )$ $\Rightarrow$ $\sigma (g)\in \ker(\varphi )$ $\Rightarrow$ $g=\sigma ^{{-1}}(\sigma (g))\in \ker(\varphi )$, since $\sigma ^{{-1}}(\ker(\varphi ))\leq \ker(\varphi )$.

Now, let us denote the canonical projection from $G$ to its abelianization $G/G^{\prime }$ by $\omega :\,G\to G/G^{\prime }$. There exists a unique induced automorphism ${\bar {\sigma }}\in {\mathrm {Aut}}(G/G^{\prime })$ such that $\omega \circ \sigma ={\bar {\sigma }}\circ \omega$, that is, ${\bar {\sigma }}(gG^{\prime })={\bar {\sigma }}(\omega (g))=\omega (\sigma (g))=\sigma (g)G^{\prime }$, for all $g\in G$. The reason for the injectivity of $\bar{\sigma}$ is that $\sigma (g)G^{\prime }={\bar {\sigma }}(gG^{\prime })=G^{\prime }$ $\Rightarrow$ $\sigma (g)\in G^{\prime }$ $\Rightarrow$ $g=\sigma ^{{-1}}(\sigma (g))\in G^{\prime }$, since $G^{\prime }$ is a characteristic subgroup of $G$.

Definition.

$G$ is called a σ-group, if there exists an automorphism $\sigma \in {\mathrm {Aut}}(G)$ such that the induced automorphism acts like the inversion on $G/G^{\prime }$, that is, $\sigma (g)G^{\prime }={\bar {\sigma }}(gG^{\prime })=g^{{-1}}G^{\prime }$, resp. $\sigma (g)\equiv g^{{-1}}{\pmod {G^{\prime }}}$, for all $g\in G$.

The supplementary inheritance property asserts that, if $G$ is a $\sigma$-group and $\sigma (\ker(\varphi ))=\ker(\varphi )$, then ${\tilde {G}}$ is also a $\sigma$-group, the required automorphism being ${\tilde {\sigma }}$.

This can be seen by applying the epimorphism $\varphi$ to the equation $\sigma (g)G^{\prime }={\bar {\sigma }}(gG^{\prime })=g^{{-1}}G^{\prime }$, for $g\in G$, which yields ${\tilde {\sigma }}(x){\tilde {G}}^{\prime }={\tilde {\sigma }}(\varphi (g)){\tilde {G}}^{\prime }=\varphi (\sigma (g))\varphi (G^{\prime })=\varphi (g^{{-1}})\varphi (G^{\prime })=\varphi (g)^{{-1}}{\tilde {G}}^{\prime }=x^{{-1}}{\tilde {G}}^{\prime }$, for all $x=\varphi (g)\in \varphi (G)={\tilde {G}}$.

Stabilization criteria

In this section, the results concerning the inheritance of TTTs and TKTs from quotients in the previous section are applied to the simplest case, which is characterized by the following

Assumption.

The parent $\pi (G)$ of a group $G$ is the quotient $\pi (G)=G/N$ of $G$ by the last non-trivial term $N=\gamma _{c}(G)\triangleleft G$ of the lower central series of $G$, where $c$ denotes the nilpotency class of $G$. The corresponding epimorphism $\pi$ from $G$ onto $\pi (G)=G/\gamma _{c}(G)$ is the canonical projection, whose kernel is given by $\ker(\pi )=\gamma _{c}(G)$.

Under this assumption, the kernels and targets of Artin transfers turn out to be compatible with parent-descendant relations between finite p-groups.

Compatibility criterion.

Let $p$ be a prime number. Suppose that $G$ is a non-abelian finite p-group of nilpotency class $c={\mathrm {cl}}(G)\geq 2$. Then the TTT and the TKT of $G$ and of its parent $\pi (G)$ are comparable in the sense that $\tau (\pi (G))\preceq \tau (G)$ and $\varkappa (G)\preceq \varkappa (\pi (G))$.

The simple reason for this fact is that, for any subgroup $G^{\prime }\leq H\leq G$, we have $\ker(\pi )=\gamma _{c}(G)\leq \gamma _{2}(G)=G^{\prime }\leq H$, since $c\geq 2$.

For the remaining part of this section, the investigated groups are supposed to be finite metabelian p-groups $G$ with elementary abelianization $G/G^{\prime }$ of rank $2$, that is of type $(p,p)$.

Partial stabilization for maximal class.

A metabelian p-group $G$ of coclass ${\mathrm {cc}}(G)=1$ and of nilpotency class $c={\mathrm {cl}}(G)\geq 3$ shares the last $p$ components of the TTT $\tau (G)$ and of the TKT $\varkappa (G)$ with its parent $\pi (G)$. More explicitly, for odd primes $p\geq 3$, we have $\tau (G)_{i}=(p,p)$ and $\varkappa (G)_{i}=0$ for $2\leq i\leq p+1$. ^[16]

This criterion is due to the fact that $c\geq 3$ implies $\ker(\pi )=\gamma _{c}(G)\leq \gamma _{3}(G)=H_{i}^{\prime }$, ^[17] for the last $p$ maximal subgroups $H_{2},\ldots ,H_{{p+1}}$ of $G$.

The condition $c\geq 3$ is indeed necessary for the partial stabilization criterion. For odd primes $p\geq 3$, the extra special $p$-group $G=G_{0}^{3}(0,1)$ of order $p^3$ and exponent $p^{2}$ has nilpotency class $c=2$ only, and the last $p$ components of its TKT $\varkappa =(1^{{p+1}})$ are strictly smaller than the corresponding components of the TKT $\varkappa =(0^{{p+1}})$ of its parent $\pi (G)$ which is the elementary abelian $p$-group of type $(p,p)$. ^[16] For $p=2$, both extra special $2$-groups of coclass $1$ and class $c=2$, the ordinary quaternion group $G=G_{0}^{3}(0,1)$ with TKT $\varkappa =(123)$ and the dihedral group $G=G_{0}^{3}(0,0)$ with TKT $\varkappa =(023)$, have strictly smaller last two components of their TKTs than their common parent $\pi (G)=C_{2}\times C_{2}$ with TKT $\varkappa =(000)$.

Total stabilization for maximal class and positive defect.

A metabelian p-group $G$ of coclass ${\mathrm {cc}}(G)=1$ and of nilpotency class $c=m-1={\mathrm {cl}}(G)\geq 4$, that is, with index of nilpotency $m\geq 5$, shares all $p+1$ components of the TTT $\tau (G)$ and of the TKT $\varkappa (G)$ with its parent $\pi (G)$, provided it has positive defect of commutativity $k=k(G)\geq 1$. ^[11] Note that $k\geq 1$ implies $p\geq 3$, and we have $\varkappa (G)_{i}=0$ for all $1\leq i\leq p+1$. ^[16]

This statement can be seen by observing that the conditions $m\geq 5$ and $k\geq 1$ imply $\ker(\pi )=\gamma _{{m-1}}(G)\leq \gamma _{{m-k}}(G)\leq H_{i}^{\prime }$, ^[17] for all the $p+1$ maximal subgroups $H_{1},\ldots ,H_{{p+1}}$ of $G$.

The condition $k\geq 1$ is indeed necessary for total stabilization. To see this it suffices to consider the first component of the TKT only. For each nilpotency class $c\geq 4$, there exist (at least) two groups $G=G_{0}^{{c+1}}(0,1)$ with TKT $\varkappa =(10^{p})$ and $G=G_{0}^{{c+1}}(1,0)$ with TKT $\varkappa =(20^{p})$, both with defect $k=0$, where the first component of their TKT is strictly smaller than the first component of the TKT $\varkappa =(0^{{p+1}})$ of their common parent $\pi (G)=G_{0}^{c}(0,0)$.

Partial stabilization for non-maximal class.

Let $p=3$ be fixed. A metabelian 3-group $G$ with abelianization $G/G^{\prime }\simeq (3,3)$, coclass ${\mathrm {cc}}(G)\geq 2$ and nilpotency class $c={\mathrm {cl}}(G)\geq 4$ shares the last two (among the four) components of the TTT $\tau (G)$ and of the TKT $\varkappa (G)$ with its parent $\pi (G)$.

This criterion is justified by the following consideration. If $c\geq 4$, then $\ker(\pi )=\gamma _{c}(G)\leq \gamma _{4}(G)\leq H_{i}^{\prime }$ ^[17] for the last two maximal subgroups $H_{3},H_{4}$ of $G$.

The condition $c\geq 4$ is indeed unavoidable for partial stabilization, since there exist several $3$-groups of class $c=3$, for instance those with SmallGroups identifiers $G\in \lbrace \langle 243,3\rangle ,\langle 243,6\rangle ,\langle 243,8\rangle \rbrace$, such that the last two components of their TKTs $\varkappa \in \lbrace (0043),(0122),(2034)\rbrace$ are strictly smaller than the last two components of the TKT $\varkappa =(0000)$ of their common parent $\pi (G)=G_{0}^{3}(0,0)$.

Total stabilization for non-maximal class and cyclic centre.

Again, let $p=3$ be fixed. A metabelian 3-group $G$ with abelianization $G/G^{\prime }\simeq (3,3)$, coclass ${\mathrm {cc}}(G)\geq 2$, nilpotency class $c={\mathrm {cl}}(G)\geq 4$ and cyclic centre $\zeta _{1}(G)$ shares all four components of the TTT $\tau (G)$ and of the TKT $\varkappa (G)$ with its parent $\pi (G)$.

The reason is that, due to the cyclic centre, we have $\ker(\pi )=\gamma _{c}(G)=\zeta _{1}(G)\leq H_{i}^{\prime }$ ^[17] for all four maximal subgroups $H_{1},\ldots ,H_{4}$ of $G$.

The condition of a cyclic centre is indeed necessary for total stabilization, since for a group with bicyclic centre there occur two possibilities. Either $\gamma _{c}(G)=\zeta _{1}(G)$ is also bicyclic, whence $\gamma _{c}(G)$ is never contained in $H_{2}^{\prime }$, or $\gamma _{c}(G)<\zeta _{1}(G)$ is cyclic but is never contained in $H_{1}^{\prime }$.

Summarizing, we can say that the last four criteria underpin the fact that Artin transfers provide a marvellous tool for classifying finite p-groups.

In the following sections, it will be shown how these ideas can be applied for endowing descendant trees with additional structure, and for searching particular groups in descendant trees by looking for patterns defined by the kernels and targets of Artin transfers. These strategies of pattern recognition are useful in pure group theory and in algebraic number theory.

Figure 4: Endowing a descendant tree with information on Artin transfers.

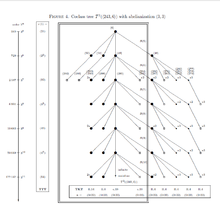
Structured descendant trees (SDTs)

This section uses the terminology of descendant trees in the theory of finite p-groups. In Figure 4, a descendant tree with modest complexity is selected exemplarily to demonstrate how Artin transfers provide additional structure for each vertex of the tree. More precisely, the underlying prime is $p=3$, and the chosen descendant tree is actually a coclass tree having a unique infinite mainline, branches of depth $3$, and strict periodicity of length $2$ setting in with branch ${\mathcal {B}}(7)$. The initial pre-period consists of branches ${\mathcal {B}}(5)$ and ${\mathcal {B}}(6)$ with exceptional structure. Branches ${\mathcal {B}}(7)$ and ${\mathcal {B}}(8)$ form the primitive period such that ${\mathcal {B}}(j)\simeq {\mathcal {B}}(7)$, for odd $j\geq 9$, and ${\mathcal {B}}(j)\simeq {\mathcal {B}}(8)$, for even $j\geq 10$. The root of the tree is the metabelian $3$-group with identifier $R=\langle 243,6\rangle$, that is, a group of order $\vert R\vert =3^{5}=243$ and with counting number $6$. It should be emphasized that this root is not coclass settled, whence its entire descendant tree ${\mathcal {T}}(R)$ is of considerably higher complexity than the coclass-$2$ subtree ${\mathcal {T}}^{2}(R)$, whose first six branches are drawn in the diagram of Figure 4. The additional structure can be viewed as a sort of coordinate system in which the tree is embedded. The horizontal abscissa is labelled with the transfer kernel type (TKT) $\varkappa$, and the vertical ordinate is labelled with a single component $\tau (1)$ of the transfer target type (TTT). The vertices of the tree are drawn in such a manner that members of periodic infinite sequences form a vertical column sharing a common TKT. On the other hand, metabelian groups of a fixed order, represented by vertices of depth at most $1$, form a horizontal row sharing a common first component of the TTT. (To discourage any incorrect interpretations, we explicitly point out that the first component of the TTT of non-metabelian groups or metabelian groups, represented by vertices of depth $2$, is usually smaller than expected, due to stabilization phenomena!) The TTT of all groups in this tree represented by a big full disk, which indicates a bicyclic centre of type $(3,3)$, is given by $\tau =\lbrack A(3,c),(3,3,3),(9,3),(9,3)\rbrack$ with varying first component $\tau (1)=A(3,c)$, the nearly homocyclic abelian $3$-group of order $3^{c}$, and fixed further components $\tau (2)=(3,3,3){\hat {=}}(1^{3})$ and $\tau (3)=\tau (4)=(9,3){\hat {=}}(21)$, where the abelian type invariants are either written as orders of cyclic components or as their $3$-logarithms with exponents indicating iteration. (The latter notation is employed in Figure 4.) Since the coclass of all groups in this tree is $2$, the connection between the order $3^{n}$ and the nilpotency class is given by $c=n-2$.

Pattern recognition

For searching a particular group in a descendant tree by looking for patterns defined by the kernels and targets of Artin transfers, it is frequently adequate to reduce the number of vertices in the branches of a dense tree with high complexity by sifting groups with desired special properties, for example

• filtering the $\sigma$-groups,
• eliminating a set of certain transfer kernel types,
• cancelling all non-metabelian groups (indicated by small contour squares in Fig. 4),
• removing metabelian groups with cyclic centre (denoted by small full disks in Fig. 4),
• cutting off vertices whose distance from the mainline (depth) exceeds some lower bound,
• combining several different sifting criteria.

The result of such a sieving procedure is called a pruned descendant tree with respect to the desired set of properties. However, in any case, it should be avoided that the main line of a coclass tree is eliminated, since the result would be a disconnected infinite set of finite graphs instead of a tree. For example, it is neither recommended to eliminate all $\sigma$-groups in Figure 4 nor to eliminate all groups with TKT $\varkappa =(0122)$. In Figure 4, the big double contour rectangle surrounds the pruned coclass tree ${\mathcal {T}}_{{\ast }}^{2}(R)$, where the numerous vertices with TKT $\varkappa =(2122)$ are completely eliminated. This would, for instance, be useful for searching a $\sigma$-group with TKT $\varkappa =(1122)$ and first component $\tau (1)=(43)$ of the TTT. In this case, the search result would even be a unique group. We expand this idea further in the following detailed discussion of an important example.

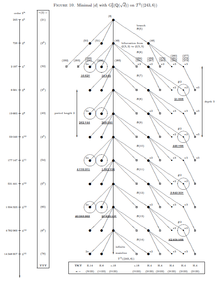
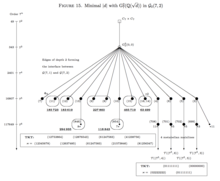
Historical example

The oldest example of searching for a finite p-group by the strategy of pattern recognition via Artin transfers goes back to 1934, when A. Scholz and O. Taussky ^[18] tried to determine the Galois group $G={\mathrm {G}}_{3}^{{\infty }}(K)={\mathrm {Gal}}({\mathrm {F}}_{3}^{{\infty }}(K)\vert K)$ of the Hilbert $3$-class field tower, that is the maximal unramified pro-$3$ extension ${\mathrm {F}}_{3}^{{\infty }}(K)$, of the complex quadratic number field $K={\mathbb {Q}}({\sqrt {-9748}})$. They actually succeeded in finding the maximal metabelian quotient $Q=G/G^{{\prime \prime }}={\mathrm {G}}_{3}^{2}(K)={\mathrm {Gal}}({\mathrm {F}}_{3}^{2}(K)\vert K)$ of $G$, that is the Galois group of the second Hilbert $3$-class field ${\mathrm {F}}_{3}^{2}(K)$ of $K$. However, it needed $78$ years until M. R. Bush and D. C. Mayer, in 2012, provided the first rigorous proof ^[15] that the (potentially infinite) $3$-tower group $G={\mathrm {G}}_{3}^{{\infty }}(K)$ coincides with the finite $3$-group ${\mathrm {G}}_{3}^{3}(K)={\mathrm {Gal}}({\mathrm {F}}_{3}^{3}(K)\vert K)$ of derived length ${\mathrm {dl}}(G)=3$, and thus the $3$-tower of $K$ has exactly three stages, stopping at the third Hilbert $3$-class field ${\mathrm {F}}_{3}^{3}(K)$ of $K$.

Table 1: Possible quotients P_c of the 3-tower group G of K ^[15]

c	order of Pc	SmallGroups identifier of Pc	TKT $\varkappa$ of Pc	TTT $\tau$ of Pc	ν	μ	descendant numbers of Pc
$1$	$9$	$\langle 9,2\rangle$	$(0000)$	$\lbrack (1)(1)(1)(1)\rbrack$	$3$	$3$	$3/2;3/3;1/1$
$2$	$27$	$\langle 27,3\rangle$	$(0000)$	$\lbrack (1^{2})(1^{2})(1^{2})(1^{2})\rbrack$	$2$	$4$	$4/1;7/5$
$3$	$243$	$\langle 243,8\rangle$	$(2034)$	$\lbrack (21)(21)(21)(21)\rbrack$	$1$	$3$	$4/4$
$4$	$729$	$\langle 729,54\rangle$	$(2034)$	$\lbrack (21)(2^{2})(21)(21)\rbrack$	$2$	$4$	$8/3;6/3$
$5$	$2187$	$\langle 2187,302\rangle$	$(2334)$	$\lbrack (21)(32)(21)(21)\rbrack$	${\displaystyle 0}$	$3$	$0/0$
$5$	$2187$	$\langle 2187,306\rangle$	$(2434)$	$\lbrack (21)(32)(21)(21)\rbrack$	${\displaystyle 0}$	$3$	$0/0$
$5$	$2187$	$\langle 2187,303\rangle$	$(2034)$	$\lbrack (21)(32)(21)(21)\rbrack$	$1$	$4$	$5/2$
$5$	$6561$	$\langle 729,54\rangle -\#2;2$	$(2334)$	$\lbrack (21)(32)(21)(21)\rbrack$	${\displaystyle 0}$	$2$	$0/0$
$5$	$6561$	$\langle 729,54\rangle -\#2;6$	$(2434)$	$\lbrack (21)(32)(21)(21)\rbrack$	${\displaystyle 0}$	$2$	$0/0$
$5$	$6561$	$\langle 729,54\rangle -\#2;3$	$(2034)$	$\lbrack (21)(32)(21)(21)\rbrack$	$1$	$3$	$4/4$
$6$	$6561$	$\langle 2187,303\rangle -\#1;1$	$(2034)$	$\lbrack (21)(3^{2})(21)(21)\rbrack$	$1$	$4$	$7/3$
$6$	$19683$	$\langle 729,54\rangle -\#2;3-\#1;1$	$(2034)$	$\lbrack (21)(3^{2})(21)(21)\rbrack$	$2$	$4$	$8/3;6/3$

The search is performed with the aid of the p-group generation algorithm by M. F. Newman ^[19] and E. A. O'Brien. ^[20] For the initialization of the algorithm, two basic invariants must be determined. Firstly, the generator rank $d$ of the p-groups to be constructed. Here, we have $p=3$ and $d=r_{3}(K)=d({\mathrm {Cl}}_{3}(K))$ is given by the $3$-class rank of the quadratic field $K$. Secondly, the abelian type invariants of the $3$-class group ${\mathrm {Cl}}_{3}(K)\simeq (1^{2})$ of $K$. These two invariants indicate the root of the descendant tree which will be constructed successively. Although the p-group generation algorithm is designed to use the parent-descendant definition by means of the lower exponent-p central series, it can be fitted to the definition with the aid of the usual lower central series. In the case of an elementary abelian p-group as root, the difference is not very big. So we have to start with the elementary abelian $3$-group of rank two, which has the SmallGroups identifier $\langle 9,2\rangle$, and to construct the descendant tree ${\mathcal {T}}(\langle 9,2\rangle )$. We do that by iterating the p-group generation algorithm, taking suitable capable descendants of the previous root as the next root, always executing an increment of the nilpotency class by a unit.

As explained at the beginning of the section Pattern recognition, we must prune the descendant tree with respect to the invariants TKT and TTT of the $3$-tower group $G$, which are determined by the arithmetic of the field $K$ as $\varkappa \in \lbrace (2334),(2434)\rbrace$ (exactly two fixed points and no transposition) and $\tau =\lbrack (21)(32)(21)(21)\rbrack$. Further, any quotient of $G$ must be a $\sigma$-group, enforced by number theoretic requirements for the quadratic field $K$.

The root $\langle 9,2\rangle$ has only a single capable descendant $\langle 27,3\rangle$ of type $(1^{2})$. In terms of the nilpotency class, $\langle 9,2\rangle$ is the class-$1$ quotient $G/\gamma _{2}(G)$ of $G$ and $\langle 27,3\rangle$ is the class-$2$ quotient $G/\gamma _{3}(G)$ of $G$. Since the latter has nuclear rank two, there occurs a bifurcation ${\mathcal {T}}(\langle 27,3\rangle )={\mathcal {T}}^{1}(\langle 27,3\rangle ){\dot {\cup }}{\mathcal {T}}^{2}(\langle 27,3\rangle )$, where the former component ${\mathcal {T}}^{1}(\langle 27,3\rangle )$ can be eliminated by the stabilization criterion $\varkappa =(\ast 000)$ for the TKT of all $3$-groups of maximal class.

Due to the inheritance property of TKTs, only the single capable descendant $\langle 243,8\rangle$ qualifies as the class-$3$ quotient $G/\gamma _{4}(G)$ of $G$. There is only a single capable $\sigma$-group $\langle 729,54\rangle$ among the descendants of $\langle 243,8\rangle$. It is the class-$4$ quotient $G/\gamma _{5}(G)$ of $G$ and has nuclear rank two.

This causes the essential bifurcation ${\mathcal {T}}(\langle 729,54\rangle )={\mathcal {T}}^{2}(\langle 729,54\rangle ){\dot {\cup }}{\mathcal {T}}^{3}(\langle 729,54\rangle )$ in two subtrees belonging to different coclass graphs ${\mathcal {G}}(3,2)$ and ${\mathcal {G}}(3,3)$. The former contains the metabelian quotient $Q=G/G^{{\prime \prime }}$ of $G$ with two possibilities $Q\in \lbrace \langle 2187,302\rangle ,\langle 2187,306\rangle \rbrace$, which are not balanced with relation rank $r=3>2=d$ bigger than the generator rank. The latter consists entirely of non-metabelian groups and yields the desired $3$-tower group $G$ as one among the two Schur $\sigma$-groups $\langle 729,54\rangle -\#2;2$ and $\langle 729,54\rangle -\#2;6$ with $r=2=d$.

Finally the termination criterion is reached at the capable vertices $\langle 2187,303\rangle -\#1;1\in {\mathcal {G}}(3,2)$ and $\langle 729,54\rangle -\#2;3-\#1;1\in {\mathcal {G}}(3,3)$, since the TTT $\tau =\lbrack (21)(3^{2})(21)(21)\rbrack >\lbrack (21)(32)(21)(21)\rbrack$ is too big and will even increase further, never returning to $\lbrack (21)(32)(21)(21)\rbrack$. The complete search process is visualized in Table 1, where, for each of the possible successive p-quotients $P_{c}=G/\gamma _{{c+1}}(G)$ of the $3$-tower group $G={\mathrm {G}}_{3}^{{\infty }}(K)$ of $K={\mathbb {Q}}({\sqrt {-9748}})$, the nilpotency class is denoted by $c={\mathrm {cl}}(P_{c})$, the nuclear rank by $\nu =\nu (P_{c})$, and the p-multiplicator rank by $\mu =\mu (P_{c})$.

Commutator calculus

This section shows exemplarily how commutator calculus can be used for determining the kernels and targets of Artin transfers explicitly. As a concrete example we take the metabelian $3$-groups with bicyclic centre, which are represented by big full disks as vertices, of the coclass tree diagram in Figure 4. They form ten periodic infinite sequences, four, resp. six, for even, resp. odd, nilpotency class $c$, and can be characterized with the aid of a parametrized polycyclic power-commutator presentation:

1 ${\begin{aligned}G^{{c,n}}(z,w)=&\langle x,y,s_{2},t_{3},s_{3},\ldots ,s_{c}\mid {}\\&x^{3}=s_{c}^{w},\ y^{3}=s_{3}^{2}s_{4}s_{c}^{z},\ s_{j}^{3}=s_{{j+2}}^{2}s_{{j+3}}{\text{ for }}2\leq j\leq c-3,\ s_{{c-2}}^{3}=s_{c}^{2},\ t_{3}^{3}=1,\\&s_{2}=\lbrack y,x\rbrack ,\ t_{3}=\lbrack s_{2},y\rbrack ,\ s_{j}=\lbrack s_{{j-1}},x\rbrack {\text{ for }}3\leq j\leq c\rangle ,\end{aligned}}$

where $c\geq 5$ is the nilpotency class, $3^{n}$ with $n=c+2$ is the order, and $0\leq w\leq 1$, $-1\leq z\leq 1$ are parameters.

The transfer target type (TTT) of the group $G=G^{{c,n}}(z,w)$ depends only on the nilpotency class $c$, is independent of the parameters $w,z$, and is given uniformly by $\tau =\lbrack A(3,c),(3,3,3),(9,3),(9,3)\rbrack$. This phenomenon is called a polarization, more precisely a uni-polarization, ^[11] at the first component.

The transfer kernel type (TKT) of the group $G=G^{{c,n}}(z,w)$ is independent of the nilpotency class $c$, but depends on the parameters $w,z$, and is given by c.18, $\varkappa =(0122)$, for $w=z=0$ (a mainline group), H.4, $\varkappa =(2122)$, for $w=0,z=\pm 1$ (two capable groups), E.6, $\varkappa =(1122)$, for $w=1,z=0$ (a terminal group), and E.14, $\varkappa \in \lbrace (4122),(3122)\rbrace$, for $w=1,z=\pm 1$ (two terminal groups). For even nilpotency class, the two groups of types H.4 and E.14, which differ in the sign of the parameter $z$ only, are isomorphic.

These statements can be deduced by means of the following considerations.

As a preparation, it is useful to compile a list of some commutator relations, starting with those given in the presentation, $\lbrack a,x\rbrack =1$ for $a\in \lbrace s_{c},t_{3}\rbrace$ and $\lbrack a,y\rbrack =1$ for $a\in \lbrace s_{3},\ldots ,s_{c},t_{3}\rbrace$, which shows that the bicyclic centre is given by $\zeta _{1}(G)=\langle s_{c},t_{3}\rangle$. By means of the right product rule $\lbrack a,xy\rbrack =\lbrack a,y\rbrack \cdot \lbrack a,x\rbrack \cdot \lbrack \lbrack a,x\rbrack ,y\rbrack$ and the right power rule $\lbrack a,y^{2}\rbrack =\lbrack a,y\rbrack ^{{1+y}}$, we obtain $\lbrack s_{2},xy\rbrack =s_{3}t_{3}$, $\lbrack s_{2},xy^{2}\rbrack =s_{3}t_{3}^{2}$, and $\lbrack s_{j},xy\rbrack =\lbrack s_{j},xy^{2}\rbrack =\lbrack s_{j},x\rbrack =s_{{j+1}}$, for $j\geq 3$.

The maximal subgroups of $G$ are taken in a similar way as in the section on the computational implementation, namely $H_{1}=\langle y,G^{\prime }\rangle$, $H_{2}=\langle x,G^{\prime }\rangle$, $H_{3}=\langle xy,G^{\prime }\rangle$, and $H_{4}=\langle xy^{2},G^{\prime }\rangle$.

Their derived subgroups are crucial for the behavior of the Artin transfers. By making use of the general formula $H_{i}^{\prime }=(G^{\prime })^{{h_{i}-1}}$, where $H_{i}=\langle h_{i},G^{\prime }\rangle$, and where we know that $G^{\prime }=\langle s_{2},t_{3},s_{3},\ldots ,s_{c}\rangle$ in the present situation, it follows that $H_{1}^{\prime }=\langle s_{2}^{{y-1}}\rangle =\langle t_{3}\rangle$, $H_{2}^{\prime }=\langle s_{2}^{{x-1}},\ldots ,s_{{c-1}}^{{x-1}}\rangle =\langle s_{3},\ldots ,s_{c}\rangle$, $H_{3}^{\prime }=\langle s_{2}^{{xy-1}},\ldots ,s_{{c-1}}^{{xy-1}}\rangle =\langle s_{3}t_{3},s_{4},\ldots ,s_{c}\rangle$, and $H_{4}^{\prime }=\langle s_{2}^{{xy^{2}-1}},\ldots ,s_{{c-1}}^{{xy^{2}-1}}\rangle =\langle s_{3}t_{3}^{2},s_{4},\ldots ,s_{c}\rangle$. Note that $H_{1}$ is not far from being abelian, since $H_{1}^{\prime }=\langle t_{3}\rangle$ is contained in the centre $\zeta _{1}(G)=\langle s_{c},t_{3}\rangle$.

As the first main result, we are now in the position to determine the abelian type invariants of the derived quotients: $H_{1}/H_{1}^{\prime }=\langle y,s_{2},\ldots ,s_{c}\rangle H_{1}^{\prime }/H_{1}^{\prime }\simeq A(3,c)$, the unique quotient which grows with increasing nilpotency class $c$, since ${\mathrm {ord}}(y)={\mathrm {ord}}(s_{2})=3^{m}$ for even $c=2m$ and ${\mathrm {ord}}(y)=3^{{m+1}},{\mathrm {ord}}(s_{2})=3^{m}$ for odd $c=2m+1$, $H_{2}/H_{2}^{\prime }=\langle x,s_{2},t_{3}\rangle H_{2}^{\prime }/H_{2}^{\prime }\simeq (3,3,3)$, $H_{3}/H_{3}^{\prime }=\langle xy,s_{2},t_{3}\rangle H_{3}^{\prime }/H_{3}^{\prime }\simeq (9,3)$, $H_{4}/H_{4}^{\prime }=\langle xy^{2},s_{2},t_{3}\rangle H_{4}^{\prime }/H_{4}^{\prime }\simeq (9,3)$, since generally ${\mathrm {ord}}(s_{2})={\mathrm {ord}}(t_{3})=3$, but ${\mathrm {ord}}(x)=3$ for $H_{2}$, whereas ${\mathrm {ord}}(xy)={\mathrm {ord}}(xy^{2})=9$ for $H_{3}$ and $H_{4}$.

Now we come to the kernels of the Artin transfer homomorphisms $T_{i}:\,G\to H_{i}/H_{i}^{\prime }$. It suffices to investigate the induced transfers ${\tilde {T}}_{i}:\,G/G^{\prime }\to H_{i}/H_{i}^{\prime }$ and to begin by finding expressions for the images ${\tilde {T}}_{i}(gG^{\prime })$ of elements $gG^{\prime }\in G/G^{\prime }$, which can be expressed in the form $g\equiv x^{j}y^{{\ell }}{\pmod {G^{\prime }}}$ with exponents $-1\leq j,\ell \leq 1$. First, we exploit outer transfers as much as possible: $x\notin H_{1}$ $\Rightarrow$ ${\tilde {T}}_{1}(xG^{\prime })=x^{3}H_{1}^{\prime }=s_{c}^{w}H_{1}^{\prime }$, $y\notin H_{2}$ $\Rightarrow$ ${\tilde {T}}_{2}(yG^{\prime })=y^{3}H_{2}^{\prime }=s_{3}^{2}s_{4}s_{c}^{z}H_{2}^{\prime }=1\cdot H_{2}^{\prime }$, $x,y\notin H_{3},H_{4}$ $\Rightarrow$ ${\tilde {T}}_{i}(xG^{\prime })=x^{3}H_{i}^{\prime }=s_{c}^{w}H_{i}^{\prime }=1\cdot H_{i}^{\prime }$ and ${\tilde {T}}_{i}(yG^{\prime })=y^{3}H_{i}^{\prime }=s_{3}^{2}s_{4}s_{c}^{z}H_{i}^{\prime }=s_{3}^{2}H_{i}^{\prime }$, for $3\leq i\leq 4$. Next, we treat the unavoidable inner transfers, which are more intricate. For this purpose, we use the polynomial identity $X^{2}+X+1=(X-1)^{2}+3(X-1)+3$ to obtain: $y\in H_{1}$ $\Rightarrow$ ${\tilde {T}}_{1}(yG^{\prime })=y^{{1+x+x^{2}}}H_{1}^{\prime }=y^{{3+3(x-1)+(x-1)^{2}}}H_{1}^{\prime }=y^{3}\cdot \lbrack y,x\rbrack ^{3}\cdot \lbrack \lbrack y,x\rbrack ,x\rbrack H_{1}^{\prime }$ $=s_{3}^{2}s_{4}s_{c}^{z}s_{2}^{3}s_{3}H_{1}^{\prime }=s_{2}^{3}s_{3}^{3}s_{4}s_{c}^{z}H_{1}^{\prime }=s_{c}^{z}H_{1}^{\prime }$ and $x\in H_{2}$ $\Rightarrow$ ${\tilde {T}}_{2}(xG^{\prime })=x^{{1+y+y^{2}}}H_{2}^{\prime }=x^{{3+3(y-1)+(y-1)^{2}}}H_{2}^{\prime }=x^{3}\cdot \lbrack x,y\rbrack ^{3}\cdot \lbrack \lbrack x,y\rbrack ,y\rbrack H_{2}^{\prime }=s_{c}^{w}s_{2}^{{-3}}t_{3}^{{-1}}H_{2}^{\prime }=t_{3}^{{-1}}H_{2}^{\prime }$. Finally, we combine the results: generally ${\tilde {T}}_{i}(gG^{\prime })={\tilde {T}}_{i}(xG^{\prime })^{j}{\tilde {T}}_{i}(yG^{\prime })^{{\ell }}$, and in particular, ${\tilde {T}}_{1}(gG^{\prime })=s_{c}^{{wj+z\ell }}H_{1}^{\prime }$, ${\tilde {T}}_{2}(gG^{\prime })=t_{3}^{{-j}}H_{2}^{\prime }$, ${\tilde {T}}_{i}(gG^{\prime })=s_{3}^{{2\ell }}H_{i}^{\prime }$, for $3\leq i\leq 4$. To determine the kernels, it remains to solve the following equations: $s_{c}^{{wj+z\ell }}H_{1}^{\prime }=H_{1}^{\prime }$ $\Rightarrow$ $j,\ell$ arbitrary for $w=z=0$, $\ell =0$ with arbitrary $j$ for $w=0,z=\pm 1$, $j=0$ with arbitrary $\ell$ for $w=1,z=0$, and $j=\mp \ell$ for $w=1,z=\pm 1$, furthermore, $t_{3}^{{-j}}H_{2}^{\prime }=H_{2}^{\prime }$ $\Rightarrow$ $j=0$ with arbitrary $\ell$, $s_{3}^{{2\ell }}H_{i}^{\prime }=H_{i}^{\prime }$ $\Rightarrow$ $\ell =0$ with arbitrary $j$, for $3\leq i\leq 4$. The following equivalences, for any $1\leq i\leq 4$, finish the justification of the statements: $j=0$ with arbitrary $\ell$ $\Leftrightarrow$ $\ker(T_{i})=\langle y,G^{\prime }\rangle =H_{1}$ $\Leftrightarrow$ $\varkappa (i)=1$, $\ell =0$ with arbitrary $j$ $\Leftrightarrow$ $\ker(T_{i})=\langle x,G^{\prime }\rangle =H_{2}$ $\Leftrightarrow$ $\varkappa (i)=2$, $j=\ell$ $\Leftrightarrow$ $\ker(T_{i})=\langle xy,G^{\prime }\rangle =H_{3}$ $\Leftrightarrow$ $\varkappa (i)=3$, $j=-\ell$ $\Leftrightarrow$ $\ker(T_{i})=\langle xy^{{-1}},G^{\prime }\rangle =H_{4}$ $\Leftrightarrow$ $\varkappa (i)=4$, and $j,\ell$ both arbitrary $\Leftrightarrow$ $\ker(T_{i})=\langle x,y,G^{\prime }\rangle =G$ $\Leftrightarrow$ $\varkappa (i)=0$. Consequently, the last three components of the TKT are independent of the parameters $w,z$, which means that both, the TTT and the TKT, reveal a uni-polarization at the first component.

Systematic library of SDTs

The aim of this section is to present a collection of structured coclass trees (SCTs) of finite p-groups with parametrized presentations and a succinct summary of invariants. The underlying prime $p$ is restricted to small values $p\in \lbrace 2,3,5\rbrace$. The trees are arranged according to increasing coclass $r\geq 1$ and different abelianizations within each coclass. To keep the descendant numbers manageable, the trees are pruned by eliminating vertices of depth bigger than one. Further, we omit trees where stabilization criteria enforce a common TKT of all vertices, since we do not consider such trees as structured any more. The invariants listed include

• pre-period and period length,
• depth and width of branches,
• uni-polarization, TTT and TKT,
• $\sigma$-groups.

We refrain from giving justifications for invariants, since the way how invariants are derived from presentations was demonstrated exemplarily in the section on commutator calculus

Figure 5: Structured descendant tree of 2-groups with coclass 1.

Coclass 1

For each prime $p\in \lbrace 2,3,5\rbrace$, the unique tree of p-groups of maximal class is endowed with information on TTTs and TKTs, that is, ${\mathcal {T}}^{1}(\langle 4,2\rangle )$ for $p=2$, ${\mathcal {T}}^{1}(\langle 9,2\rangle )$ for $p=3$, and ${\mathcal {T}}^{1}(\langle 25,2\rangle )$ for $p=5$. In the last case, the tree is restricted to metabelian $5$-groups.

The $2$-groups of coclass $1$ in Figure 5 can be defined by the following parametrized polycyclic pc-presentation, quite different from Blackburn's presentation. ^[10]

2 ${\begin{aligned}G^{{c,n}}(z,w)=&\langle x,y,s_{2},\ldots ,s_{c}\mid {}\\&x^{2}=s_{c}^{w},\ y^{2}=s_{c}^{z},\ s_{j}^{2}=s_{{j+1}}s_{{j+2}}{\text{ for }}2\leq j\leq c-2,\ s_{{c-1}}^{2}=s_{c},\\&s_{2}=\lbrack y,x\rbrack ,\ s_{j}=\lbrack s_{{j-1}},x\rbrack =\lbrack s_{{j-1}},y\rbrack {\text{ for }}3\leq j\leq c\rangle ,\end{aligned}}$

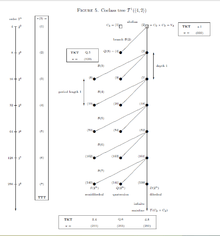
where the nilpotency class is $c\geq 3$, the order is $2^{n}$ with $n=c+1$, and $w,z$ are parameters. The branches are strictly periodic with pre-period $1$ and period length $1$, and have depth $1$ and width $3$. Polarization occurs for the third component and the TTT is $\tau =\lbrack (1^{2}),(1^{2}),A(2,c)\rbrack$, only dependent on $c$ and with cyclic $A(2,c)$. The TKT depends on the parameters and is $\varkappa =(210)$ for the dihedral mainline vertices with $w=z=0$, $\varkappa =(213)$ for the terminal generalized quaternion groups with $w=z=1$, and $\varkappa =(211)$ for the terminal semi dihedral groups with $w=1,z=0$. There are two exceptions, the abelian root with $\tau =\lbrack (1),(1),(1)\rbrack$ and $\varkappa =(000)$, and the usual quaternion group with $\tau =\lbrack (2),(2),(2)\rbrack$ and $\varkappa =(123)$.

Figure 6: Structured descendant tree of 3-groups with coclass 1.

The $3$-groups of coclass $1$ in Figure 6 can be defined by the following parametrized polycyclic pc-presentation, slightly different from Blackburn's presentation. ^[10]

3 ${\begin{aligned}G_{a}^{{c,n}}(z,w)=&\langle x,y,s_{2},t_{3},s_{3},\ldots ,s_{c}\mid {}\\&x^{3}=s_{c}^{w},\ y^{3}=s_{3}^{2}s_{4}s_{c}^{z},\ t_{3}=s_{c}^{a},\ s_{j}^{3}=s_{{j+2}}^{2}s_{{j+3}}{\text{ for }}2\leq j\leq c-3,\ s_{{c-2}}^{3}=s_{c}^{2},\\&s_{2}=\lbrack y,x\rbrack ,\ t_{3}=\lbrack s_{2},y\rbrack ,\ s_{j}=\lbrack s_{{j-1}},x\rbrack {\text{ for }}3\leq j\leq c\rangle ,\end{aligned}}$

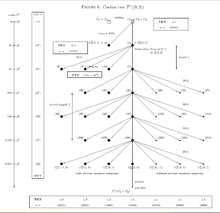
where the nilpotency class is $c\geq 5$, the order is $3^{n}$ with $n=c+1$, and $a,w,z$ are parameters. The branches are strictly periodic with pre-period $2$ and period length $2$, and have depth $1$ and width $7$. Polarization occurs for the first component and the TTT is $\tau =\lbrack A(3,c-a),(1^{2}),(1^{2}),(1^{2})\rbrack$, only dependent on $c$ and $a$. The TKT depends on the parameters and is $\varkappa =(0000)$ for the mainline vertices with $a=w=z=0$, $\varkappa =(1000)$ for the terminal vertices with $a=0,w=1,z=0$, $\varkappa =(2000)$ for the terminal vertices with $a=w=0,z=\pm 1$, and $\varkappa =(0000)$ for the terminal vertices with $a=1,w\in \lbrace -1,0,1\rbrace ,z=0$. There exist three exceptions, the abelian root with $\tau =\lbrack (1),(1),(1),(1)\rbrack$, the extra special group of exponent $9$ with $\tau =\lbrack (1^{2}),(2),(2),(2)\rbrack$ and $\varkappa =(1111)$, and the Sylow $3$-subgroup of the alternating group $A_{9}$ with $\tau =\lbrack (1^{3}),(1^{2}),(1^{2}),(1^{2})\rbrack$. Mainline vertices and vertices on odd branches are $\sigma$-groups.

Figure 7: Structured descendant tree of metabelian 5-groups with coclass 1.

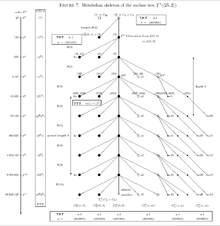
The metabelian $5$-groups of coclass $1$ in Figure 7 can be defined by the following parametrized polycyclic pc-presentation, slightly different from Miech's presentation. ^[21]

4 ${\begin{aligned}G_{a}^{{c,n}}(z,w)=&\langle x,y,s_{2},t_{3},s_{3},\ldots ,s_{c}\mid {}\\&x^{5}=s_{c}^{w},\ y^{5}=s_{c}^{z},\ t_{3}=s_{c}^{a},\\&s_{2}=\lbrack y,x\rbrack ,\ t_{3}=\lbrack s_{2},y\rbrack ,\ s_{j}=\lbrack s_{{j-1}},x\rbrack {\text{ for }}3\leq j\leq c\rangle ,\end{aligned}}$

where the nilpotency class is $c\geq 3$, the order is $5^{n}$ with $n=c+1$, and $a,w,z$ are parameters. The (metabelian!) branches are strictly periodic with pre-period $3$ and period length $4$, and have depth $3$ and width $67$. (The branches of the complete tree, including non-metabelian groups, are only virtually periodic and have bounded width but unbounded depth!) Polarization occurs for the first component and the TTT is $\tau =\lbrack A(5,c-k),(1^{2})^{5}\rbrack$, only dependent on $c$ and the defect of commutativity $k$. The TKT depends on the parameters and is $\varkappa =(0^{6})$ for the mainline vertices with $a=w=z=0$, $\varkappa =(10^{5})$ for the terminal vertices with $a=0,w=1,z=0$, $\varkappa =(20^{5})$ for the terminal vertices with $a=w=0,z\neq 0$, and $\varkappa =(0^{6})$ for the vertices with $a\neq 0$. There exist three exceptions, the abelian root with $\tau =\lbrack (1)^{6}\rbrack$, the extra special group of exponent $25$ with $\tau =\lbrack (1^{2}),(2)^{5}\rbrack$ and $\varkappa =(1^{6})$, and the group $\langle 15625,631\rangle$ with $\tau =\lbrack (1^{5}),(1^{2})^{5}\rbrack$. Mainline vertices and vertices on odd branches are $\sigma$-groups.

Coclass 2

Abelianization of type (p,p)

Three coclass trees, ${\mathcal {T}}^{2}(\langle 243,6\rangle )$, ${\mathcal {T}}^{2}(\langle 243,8\rangle )$ and ${\mathcal {T}}^{2}(\langle 729,40\rangle )$ for $p=3$, are endowed with information concerning TTTs and TKTs.

Figure 8: First structured descendant tree of 3-groups with coclass 2 and abelianization (3,3).

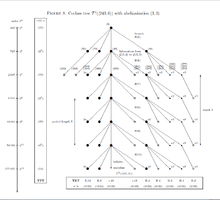
On the tree ${\mathcal {T}}^{2}(\langle 243,6\rangle )$, the $3$-groups of coclass $2$ with bicyclic centre in Figure 8 can be defined by the following parametrized polycyclic pc-presentation. ^[11]

5 ${\begin{aligned}G^{{c,n}}(z,w)=&\langle x,y,s_{2},t_{3},s_{3},\ldots ,s_{c}\mid {}\\&x^{3}=s_{c}^{w},\ y^{3}=s_{3}^{2}s_{4}s_{c}^{z},\ s_{j}^{3}=s_{{j+2}}^{2}s_{{j+3}}{\text{ for }}2\leq j\leq c-3,\ s_{{c-2}}^{3}=s_{c}^{2},\ t_{3}^{3}=1,\\&s_{2}=\lbrack y,x\rbrack ,\ t_{3}=\lbrack s_{2},y\rbrack ,\ s_{j}=\lbrack s_{{j-1}},x\rbrack {\text{ for }}3\leq j\leq c\rangle ,\end{aligned}}$

where the nilpotency class is $c\geq 5$, the order is $3^{n}$ with $n=c+2$, and $w,z$ are parameters. The branches are strictly periodic with pre-period $2$ and period length $2$, and have depth $3$ and width $18$. Polarization occurs for the first component and the TTT is $\tau =\lbrack A(3,c),(1^{3}),(21),(21)\rbrack$, only dependent on $c$. The TKT depends on the parameters and is $\varkappa =(0122)$ for the mainline vertices with $w=z=0$, $\varkappa =(2122)$ for the capable vertices with $w=0,z=\pm 1$, $\varkappa =(1122)$ for the terminal vertices with $w=1,z=0$, and $\varkappa =(3122)$ for the terminal vertices with $w=1,z=\pm 1$. Mainline vertices and vertices on even branches are $\sigma$-groups.

Figure 9: Second structured descendant tree of 3-groups with coclass 2 and abelianization (3,3).

On the tree ${\mathcal {T}}^{2}(\langle 243,8\rangle )$, the $3$-groups of coclass $2$ with bicyclic centre in Figure 9 can be defined by the following parametrized polycyclic pc-presentation. ^[11]

6 ${\begin{aligned}G^{{c,n}}(z,w)=&\langle x,y,t_{2},s_{3},t_{3},\ldots ,t_{c}\mid {}\\&y^{3}=s_{3}t_{c}^{w},\ x^{3}=t_{3}t_{4}^{2}t_{5}t_{c}^{z},\ t_{j}^{3}=t_{{j+2}}^{2}t_{{j+3}}{\text{ for }}2\leq j\leq c-3,\ t_{{c-2}}^{3}=t_{c}^{2},\ s_{3}^{3}=1,\\&t_{2}=\lbrack y,x\rbrack ,\ s_{3}=\lbrack t_{2},x\rbrack ,\ t_{j}=\lbrack t_{{j-1}},y\rbrack {\text{ for }}3\leq j\leq c\rangle ,\end{aligned}}$

where the nilpotency class is $c\geq 6$, the order is $3^{n}$ with $n=c+2$, and $w,z$ are parameters. The branches are strictly periodic with pre-period $2$ and period length $2$, and have depth $3$ and width $16$. Polarization occurs for the second component and the TTT is $\tau =\lbrack (21),A(3,c),(21),(21)\rbrack$, only dependent on $c$. The TKT depends on the parameters and is $\varkappa =(2034)$ for the mainline vertices with $w=z=0$, $\varkappa =(2134)$ for the capable vertices with $w=0,z=\pm 1$, $\varkappa =(2234)$ for the terminal vertices with $w=1,z=0$, and $\varkappa =(2334)$ for the terminal vertices with $w=1,z=\pm 1$. Mainline vertices and vertices on even branches are $\sigma$-groups.

Abelianization of type (p²,p)

${\mathcal {T}}^{2}(\langle 16,3\rangle )$ and ${\mathcal {T}}^{2}(\langle 16,4\rangle )$ for $p=2$, ${\mathcal {T}}^{2}(\langle 243,15\rangle )$ and ${\mathcal {T}}^{2}(\langle 243,17\rangle )$ for $p=3$.

Abelianization of type (p,p,p)

${\mathcal {T}}^{2}(\langle 16,11\rangle )$ for $p=2$, and ${\mathcal {T}}^{2}(\langle 81,12\rangle )$ for $p=3$.

Coclass 3

Abelianization of type (p²,p)

${\mathcal {T}}^{3}(\langle 729,13\rangle )$, ${\mathcal {T}}^{3}(\langle 729,18\rangle )$ and ${\mathcal {T}}^{3}(\langle 729,21\rangle )$ for $p=3$.

Abelianization of type (p,p,p)

${\mathcal {T}}^{3}(\langle 32,35\rangle )$ and ${\mathcal {T}}^{3}(\langle 64,181\rangle )$ for $p=2$, ${\mathcal {T}}^{3}(\langle 243,38\rangle )$ and ${\mathcal {T}}^{3}(\langle 243,41\rangle )$ for $p=3$.

Figure 10: Minimal discriminants for the first ASCT of 3-groups with coclass 2 and abelianization (3,3).

Arithmetical applications

In algebraic number theory and class field theory, structured descendant trees (SDTs) of finite p-groups provide an excellent tool for

• visualizing the location of various non-abelian p-groups $G(K)$ associated with algebraic number fields $K$,
• displaying additional information about the groups $G(K)$ in labels attached to corresponding vertices, and
• emphasizing the periodicity of occurrences of the groups $G(K)$ on branches of coclass trees.

For instance, let $p$ be a prime number, and assume that $F_{p}^{2}(K)$ denotes the second Hilbert p-class field of an algebraic number field $K$, that is the maximal metabelian unramified extension of $K$ of degree a power of $p$. Then the second p-class group $G_{p}^{2}(K)={\mathrm {Gal}}(F_{p}^{2}(K)\vert K)$ of $K$ is usually a non-abelian p-group of derived length $2$ and frequently permits to draw conclusions about the entire p-class field tower of $K$, that is the Galois group $G_{p}^{{\infty }}(K)={\mathrm {Gal}}(F_{p}^{{\infty }}(K)\vert K)$ of the maximal unramified pro-p extension $F_{p}^{{\infty }}(K)$ of $K$.

Given a sequence of algebraic number fields $K$ with fixed signature $(r_{1},r_{2})$, ordered by the absolute values $\vert d\vert$ of their discriminants $d=d(K)$, a suitable structured coclass tree (SCT) ${\mathcal {T}}$, or also the finite sporadic part ${\mathcal {G}}_{0}(p,r)$ of a coclass graph ${\mathcal {G}}(p,r)$, whose vertices are entirely or partially realized by second p-class groups $G_{p}^{2}(K)$ of the fields $K$ is endowed with additional arithmetical structure when each realized vertex $V\in {\mathcal {T}}$, resp. $V\in {\mathcal {G}}_{0}(p,r)$, is mapped to data concerning the fields $K$ such that $V=G_{p}^{2}(K)$.

Figure 11: Minimal discriminants for the second ASCT of 3-groups with coclass 2 and abelianization (3,3).

Example

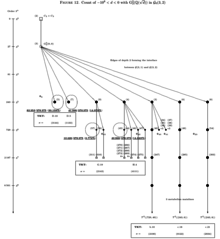
To be specific, let $p=3$ and consider complex quadratic fields $K(d)={\mathbb {Q}}({\sqrt {d}})$ with fixed signature $(0,1)$ having $3$-class groups with type invariants $(3,3)$. See OEIS A242863 . Their second $3$-class groups $G_{3}^{2}(K)$ have been determined by D. C. Mayer ^[17] for the range $-10^{6}<d<0$, and, most recently, by N. Boston, M. R. Bush and F. Hajir ^[22] for the extended range $-10^{8}<d<0$.

Let us firstly select the two structured coclass trees (SCTs) ${\mathcal {T}}^{2}(\langle 243,6\rangle )$ and ${\mathcal {T}}^{2}(\langle 243,8\rangle )$, which are known from Figures 8 and 9 already, and endow these trees with additional arithmetical structure by surrounding a realized vertex $V$ with a circle and attaching an adjacent underlined boldface integer $\min \lbrace \vert d\vert \mid V=G_{3}^{2}(K(d))\rbrace$ which gives the minimal absolute discriminant such that $V$ is realized by the second $3$-class group $G_{3}^{2}(K(d))$. Then we obtain the arithmetically structured coclass trees (ASCTs) in Figures 10 and 11, which, in particular, give an impression of the actual distribution of second $3$-class groups. ^[11] See OEIS A242878 .

Table 2: Minimal absolute discriminants for states of six sequences

State $\uparrow ^{n}$	TKT E.14 $\varkappa =(3122)$	TKT E.6 $\varkappa =(1122)$	TKT H.4 $\varkappa =(2122)$	TKT E.9 $\varkappa =(2334)$	TKT E.8 $\varkappa =(2234)$	TKT G.16 $\varkappa =(2134)$
GS $\uparrow ^{0}$	$16\,627$	$15\,544$	$21\,668$	$9\,748$	$34\,867$	$17\,131$
ES1 $\uparrow ^{1}$	$262\,744$	$268\,040$	$446\,788$	$297\,079$	$370\,740$	$819\,743$
ES2 $\uparrow ^{2}$	$4\,776\,071$	$1\,062\,708$	$3\,843\,907$	$1\,088\,808$	$4\,087\,295$	$2\,244\,399$
ES3 $\uparrow ^{3}$	$40\,059\,363$	$27\,629\,107$	$52\,505\,588$	$11\,091\,140$	$19\,027\,947$	$30\,224\,744$
ES4 $\uparrow ^{4}$				$94\,880\,548$

Concerning the periodicity of occurrences of second $3$-class groups $G_{3}^{2}(K(d))$ of complex quadratic fields, it was proved ^[17] that only every other branch of the trees in Figures 10 and 11 can be populated by these metabelian $3$-groups and that the distribution sets in with a ground state (GS) on branch ${\mathcal {B}}(6)$ and continues with higher excited states (ES) on the branches ${\mathcal {B}}(j)$ with even $j\geq 8$. This periodicity phenomenon is underpinned by three sequences with fixed TKTs ^[16]

• E.14 $\varkappa =(3122)$, OEIS A247693 ,
• E.6 $\varkappa =(1122)$, OEIS A247692 ,
• H.4 $\varkappa =(2122)$, OEIS A247694

on the ASCT ${\mathcal {T}}^{2}(\langle 243,6\rangle )$, and by three sequences with fixed TKTs ^[16]

• E.9 $\varkappa =(2334)$, OEIS A247696 ,
• E.8 $\varkappa =(2234)$, OEIS A247695 ,
• G.16 $\varkappa =(2134)$,OEIS A247697

on the ASCT ${\mathcal {T}}^{2}(\langle 243,8\rangle )$. Up to now, ^[22] the ground state and three excited states are known for each of the six sequences, and for TKT E.9 $\varkappa =(2334)$ even the fourth excited state occurred already. The minimal absolute discriminants of the various states of each of the six periodic sequences are presented in Table 2. Data for the ground states (GS) and the first excited states (ES1) has been taken from D. C. Mayer, ^[17] most recent information on the second, third and fourth excited states (ES2, ES3, ES4) is due to N. Boston, M. R. Bush and F. Hajir. ^[22]

Figure 12: Frequency of sporadic 3-groups with coclass 2 and abelianization (3,3).

Table 3: Absolute and relative frequencies of four sporadic $3$-groups

$\vert d\vert$ <	Total $\#$	TKT D.10 $\varkappa =(3144)$ $\tau =\lbrack (21)(1^{3})(21)(21)\rbrack$ $G=\langle 243,5\rangle$	TKT D.5 $\varkappa =(1133)$ $\tau =\lbrack (21)(1^{3})(21)(1^{3})\rbrack$ $G=\langle 243,7\rangle$	TKT H.4 $\varkappa =(4111)$ $\tau =\lbrack (1^{3})(1^{3})(1^{3})(21)\rbrack$ $G=\langle 729,45\rangle$	TKT G.19 $\varkappa =(2143)$ $\tau =\lbrack (21)(21)(21)(21)\rbrack$ $G=\langle 729,57\rangle$
$b=10^{6}$	$2\,020$	$667\ (33.0\%)$	$269\ (13.3\%)$	$297\ (14.7\%)$	$94\ (4.7\%)$
$b=10^{7}$	$24\,476$	$7\,622\ (31.14\%)$	$3\,625\ (14.81\%)$	$3\,619\ (14.79\%)$	$1\,019\ (4.163\%)$
$b=10^{8}$	$276\,375$	$83\,353\ (30.159\%)$	$41\,398\ (14.979\%)$	$40\,968\ (14.823\%)$	$10\,426\ (3.7724\%)$

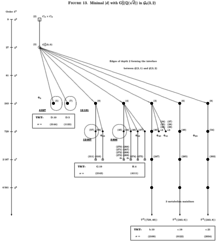
In contrast, let us secondly select the sporadic part ${\mathcal {G}}_{0}(3,2)$ of the coclass graph ${\mathcal {G}}(3,2)$ for demonstrating that another way of attaching additional arithmetical structure to descendant trees is to display the counter $\#\lbrace \vert d\vert <b\mid V=G_{3}^{2}(K(d))\rbrace$ of hits of a realized vertex $V$ by the second $3$-class group $G_{3}^{2}(K(d))$ of fields with absolute discriminants below a given upper bound $b$, for instance $b=10^{8}$. With respect to the total counter $276\,375$ of all complex quadratic fields with $3$-class group of type $(3,3)$ and discriminant $-b<d<0$, this gives the relative frequency as an approximation to the asymptotic density of the population in Figure 12 and Table 3. Exactly four vertices of the finite sporadic part ${\mathcal {G}}_{0}(3,2)$ of ${\mathcal {G}}(3,2)$ are populated by second $3$-class groups $G_{3}^{2}(K(d))$:

• $\langle 243,5\rangle$, OEIS A247689 ,
• $\langle 243,7\rangle$, OEIS A247690 ,
• $\langle 729,45\rangle$, OEIS A242873 ,
• $\langle 729,57\rangle$, OEIS A247688 .

Figure 13: Minimal absolute discriminants of sporadic 3-groups with coclass 2 and abelianization (3,3).

Figure 14: Minimal absolute discriminants of sporadic 5-groups with coclass 2 and abelianization (5,5).

Figure 15: Minimal absolute discriminants of sporadic 7-groups with coclass 2 and abelianization (7,7).

Comparison of various primes

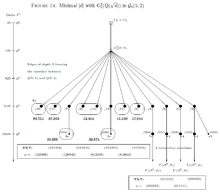
Now let $p\in \lbrace 3,5,7\rbrace$ and consider complex quadratic fields $K(d)={\mathbb {Q}}({\sqrt {d}})$ with fixed signature $(0,1)$ and p-class groups of type $(p,p)$. The dominant part of the second p-class groups of these fields populates the top vertices of order $p^{5}$ of the sporadic part ${\mathcal {G}}_{0}(p,2)$ of the coclass graph ${\mathcal {G}}(p,2)$, which belong to the stem of P. Hall's isoclinism family $\Phi _{6}$, or their immediate descendants of order $p^{6}$. For primes $p>3$, the stem of $\Phi _{6}$ consists of $p+7$ regular p-groups and reveals a rather uniform behaviour with respect to TKTs and TTTs, but the seven $3$-groups in the stem of $\Phi _{6}$ are irregular. We emphasize that there also exist several ($3$ for $p=3$ and $4$ for $p>3$) infinitely capable vertices in the stem of $\Phi _{6}$ which are partially roots of coclass trees. However, here we focus on the sporadic vertices which are either isolated Schur $\sigma$-groups ($2$ for $p=3$ and $p+1$ for $p>3$) or roots of finite trees within ${\mathcal {G}}_{0}(p,2)$ ($2$ for each $p\geq 3$). For $p>3$, the TKT of Schur $\sigma$-groups is a permutation whose cycle decomposition does not contain transpositions, whereas the TKT of roots of finite trees is a compositum of disjoint transpositions having an even number (${\displaystyle 0}$ or $2$) of fixed points.

We endow the forest ${\mathcal {G}}_{0}(p,2)$ (a finite union of descendant trees) with additional arithmetical structure by attaching the minimal absolute discriminant $\min \lbrace \vert d\vert \mid V=G_{p}^{2}(K(d))\rbrace$ to each realized vertex $V\in {\mathcal {G}}_{0}(p,2)$. The resulting structured sporadic coclass graph is shown in Figure 13 for $p=3$, in Figure 14 for $p=5$, and in Figure 15 for $p=7$.

References

1. Huppert, B. (1979). Endliche Gruppen I. Grundlehren der mathematischen Wissenschaften, Vol. 134, Springer-Verlag Berlin Heidelberg New York.
2. Schur, I. (1902). "Neuer Beweis eines Satzes über endliche Gruppen". Sitzungsb. Preuss. Akad. Wiss.: 1013–1019.
3. Artin, E. (1929). "Idealklassen in Oberkörpern und allgemeines Reziprozitätsgesetz". Abh. Math. Sem. Univ. Hamburg. 7: 46–51.
4. Isaacs, I. M. (2008). Finite group theory. Graduate Studies in Mathematics, Vol. 92, American Mathematical Society, Providence, Rhode Island.
5. Gorenstein, D. (2012). Finite groups. AMS Chelsea Publishing, American Mathematical Society, Providence, Rhode Island.
6. Hasse, H. (1930). "Bericht über neuere Untersuchungen und Probleme aus der Theorie der algebraischen Zahlkörper. Teil II: Reziprozitätsgesetz". Jahresber. Deutsch. Math. Verein., Ergänzungsband. 6: 1–204.
7. Hall M., jr. (1999). The theory of groups. AMS Chelsea Publishing, American Mathematical Society, Providence, Rhode Island.
8. Aschbacher, M. (1986). Finite group theory. Cambridge Studies in Advanced Mathematics, Vol. 10, Cambridge University Press.
9. Smith, G.; Tabachnikova, O. (2000). Topics in group theory. Springer Undergraduate Mathematics Series (SUMS), Springer-Verlag, London.
10. Blackburn, N. (1958). "On a special class of p-groups". Acta Math. 100: 45–92. doi:10.1007/bf02559602.
11. Mayer, D. C. (2013). "The distribution of second p-class groups on coclass graphs". J. Théor. Nombres Bordeaux. 25 (2): 401–456. doi:10.5802/jtnb.842.
12. Chang, S. M.; Foote, R. (1980). "Capitulation in class field extensions of type (p,p)". Can. J. Math. 32 (5): 1229–1243. doi:10.4153/cjm-1980-091-9.
13. Besche, H. U.; Eick, B.; O'Brien, E. A. (2005). The SmallGroups Library – a library of groups of small order. An accepted and refereed GAP 4 package, available also in MAGMA.
14. Besche, H. U.; Eick, B.; O'Brien, E. A. (2002). "A millennium project: constructing small groups". Int. J. Algebra Comput. 12: 623–644. doi:10.1142/s0218196702001115.
15. Bush, M. R.; Mayer, D. C. (2015). "3-class field towers of exact length 3". J. Number Theory. 147: 766–777 (preprint: arXiv:1312.0251 [math.NT], 2013). doi:10.1016/j.jnt.2014.08.010.
16. Mayer, D. C. (2012). "Transfers of metabelian p-groups". Monatsh. Math. 166 (3-4): 467–495. doi:10.1007/s00605-010-0277-x.
17. Mayer, D. C. (2012). "The second p-class group of a number field". Int. J. Number Theory. 8 (2): 471–505. doi:10.1142/s179304211250025x.
18. Scholz, A.; Taussky, O. (1934). "Die Hauptideale der kubischen Klassenkörper imaginär quadratischer Zahlkörper: ihre rechnerische Bestimmung und ihr Einfluß auf den Klassenkörperturm". J. Reine Angew. Math. 171: 19–41.
19. Newman, M. F. (1977). Determination of groups of prime-power order. pp. 73-84, in: Group Theory, Canberra, 1975, Lecture Notes in Math., Vol. 573, Springer, Berlin.
20. O'Brien, E. A. (1990). "The p-group generation algorithm". J. Symbolic Comput. 9: 677–698. doi:10.1016/s0747-7171(08)80082-x.
21. Miech, R. J. (1970). "Metabelian p-groups of maximal class". Trans. Amer. Math. Soc. 152: 331–373. doi:10.1090/s0002-9947-1970-0276343-7.
22. Boston, N.; Bush, M. R.; Hajir, F. (2015). "Heuristics for p-class towers of imaginary quadratic fields". Math. Ann. arXiv:1111.4679v2.