Banach bundle (non-commutative geometry)
In mathematics, a Banach bundle is a fiber bundle over a topological Hausdorff space, such that each fiber has the structure of a Banach space.
Definition
Let 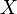 be a topological Hausdorff space, a (continuous) Banach bundle over
be a topological Hausdorff space, a (continuous) Banach bundle over 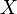 is a tuple
is a tuple 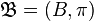 , where
, where 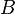 is a topological Hausdorff space, and
is a topological Hausdorff space, and 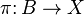 is a continuous, open surjection, such that each fiber
is a continuous, open surjection, such that each fiber 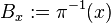 is a Banach space. Which satisfies the following conditions:
is a Banach space. Which satisfies the following conditions:
- The map
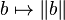 is continuous for all
is continuous for all 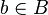
- The operation
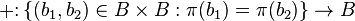 is continuous
is continuous - For every
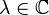 , the map
, the map 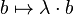 is continuous
is continuous - If
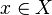 , and
, and 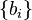 is a net in
is a net in 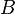 , such that
, such that 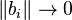 and
and 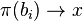 , then
, then 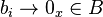 . Where
. Where 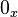 denotes the zero of the fiber
denotes the zero of the fiber 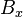 .[1]
.[1]
If the map 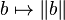 is only upper semi-continuous,
is only upper semi-continuous, 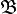 is called upper semi-continuous bundle.
is called upper semi-continuous bundle.
Examples
Trivial bundle
Let A be a Banach space, X be a topological Hausdorff space. Define 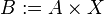 and
and 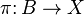 by
by 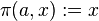 . Then
. Then 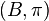 is a Banach bundle, called the trivial bundle
is a Banach bundle, called the trivial bundle
See also
- Banach bundles in differential geometry
References
- ↑ Fell, M.G., Doran, R.S.: "Representations of *-Algebras, Locally Compact Groups, and Banach *-Algebraic Bundles, Vol. 1"
This article is issued from Wikipedia - version of the 1/9/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.