Belevitch's theorem
Belevitch's theorem is a theorem in electrical network analysis due to the Russo-Belgian mathematician Vitold Belevitch (1921–1999). The theorem provides a test for a given S-matrix to determine whether or not it can be constructed as a lossless rational two-port network.
Lossless implies that the network contains only inductances and capacitances - no resistances. Rational (meaning the driving point impedance Z(p) is a rational function of p) implies that the network consists solely of discrete elements (inductors and capacitors only - no distributed elements).
The theorem
For a given S-matrix 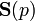 of degree
of degree 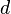 ;
;
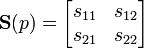
- where,
- p is the complex frequency variable and may be replaced by
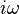 in the case of steady state sine wave signals, that is, where only a Fourier analysis is required
in the case of steady state sine wave signals, that is, where only a Fourier analysis is required - d will equate to the number of elements (inductors and capacitors) in the network, if such network exists.
Belevitch's theorem states that, 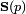 represents a lossless rational network if and only if,[1]
represents a lossless rational network if and only if,[1]
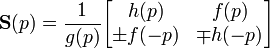
- where,
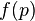 ,
, 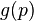 and
and 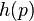 are real polynomials
are real polynomials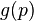 is a strict Hurwitz polynomial of degree not exceeding
is a strict Hurwitz polynomial of degree not exceeding 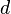
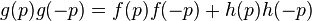 for all
for all 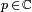 .
.
References
- ↑ Rockmore et al., pp.35-36
Bibliography
- Belevitch, Vitold Classical Network Theory, San Francisco: Holden-Day, 1968 OCLC 413916.
- Rockmore, Daniel Nahum; Healy, Dennis M. Modern Signal Processing, Cambridge: Cambridge University Press, 2004 ISBN 0-521-82706-X.
This article is issued from Wikipedia - version of the 3/22/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.