Beppo-Levi space
In functional analysis, a branch of mathematics, a Beppo-Levi space, named after Beppo Levi, is a certain space of generalized functions.
In the following, D′ is the space of distributions, S′ is the space of tempered distributions in Rn, Dα the differentiation operator with α a multi-index, and 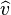 is the Fourier transform of v.
is the Fourier transform of v.
The Beppo-Levi space is
where |⋅|r,p denotes the Sobolev semi-norm.
An alternative definition is as follows: let m ∈ N, s ∈ R such that
and define:
Then Xm,s is the Beppo-Levi space.
References
- Wendland, Holger (2005), Scattered Data Approximation, Cambridge University Press.
- Rémi Arcangéli; María Cruz López de Silanes; Juan José Torrens (2007), "An extension of a bound for functions in Sobolev spaces, with applications to (m,s)-spline interpolation and smoothing" Numerische Mathematik
- Rémi Arcangéli; María Cruz López de Silanes; Juan José Torrens (2009), "Estimates for functions in Sobolev spaces defined on unbounded domains" Journal of Approximation Theory
This article is issued from Wikipedia - version of the 2/17/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
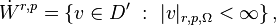
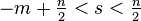
![\begin{align}
H^s &= \left \{ v \in S' \ : \ \widehat{v} \in L^1_\text{loc}(\mathbf{R}^n), \int_{\mathbf{R}^n} |\xi|^{2s}| \widehat{v} (\xi)|^2 \, d\xi < \infty \right \} \\ [6pt]
X^{m,s} &= \left \{ v \in D' \ : \ \forall \alpha \in \mathbf{N}^n, |\alpha| = m, D^{\alpha} v \in H^s \right \} \\
\end{align}](../I/m/d8d914405d94a573d9ce273530753579.png)