Biconnected graph
In graph theory, a biconnected graph is a connected and "nonseparable" graph, meaning that if any vertex were to be removed, the graph will remain connected. Therefore a biconnected graph has no articulation vertices.
The property of being 2-connected is equivalent to biconnectivity, with the caveat that the complete graph of two vertices is sometimes regarded as biconnected but not 2-connected.
This property is especially useful in maintaining a graph with a two-fold redundancy, to prevent disconnection upon the removal of a single edge (or connection).
The use of biconnected graphs is very important in the field of networking (see Network flow), because of this property of redundancy.
Definition
A biconnected undirected graph is a connected graph that is not broken into disconnected pieces by deleting any single vertex (and its incident edges).
A biconnected directed graph is one such that for any two vertices v and w there are two directed paths from v to w which have no vertices in common other than v and w.
| Vertices | Number of Possibilities |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 1 |
| 4 | 3 |
| 5 | 10 |
| 6 | 56 |
| 7 | 468 |
| 8 | 7123 |
| 9 | 194066 |
| 10 | 9743542 |
| 11 | 900969091 |
| 12 | 153620333545 |
| 13 | 48432939150704 |
| 14 | 28361824488394169 |
| 15 | 30995890806033380784 |
| 16 | 63501635429109597504951 |
| 17 | 244852079292073376010411280 |
| 18 | 1783160594069429925952824734641 |
| 19 | 24603887051350945867492816663958981 |
Examples
-
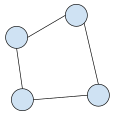
A biconnected graph on four vertices and four edges
-

A graph that is not biconnected. The removal of vertex x would disconnect the graph.
-

A biconnected graph on five vertices and six edges
-

A graph that is not biconnected. The removal of vertex x would disconnect the graph.
See also
References
- Eric W. Weisstein. "Biconnected Graph." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/BiconnectedGraph.html
- Paul E. Black, "biconnected graph", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed., U.S. National Institute of Standards and Technology. 17 December 2004. (accessed TODAY) Available from: https://xlinux.nist.gov/dads/HTML/biconnectedGraph.html
External links
- The tree of the biconnected components Java implementation in the jBPT library (see BCTree class).