Burgers' equation
Burgers' equation is a fundamental partial differential equation occurring in various areas of applied mathematics, such as fluid mechanics,[1] nonlinear acoustics,[2] gas dynamics, traffic flow. It is named for Johannes Martinus Burgers (1895–1981).
For a given field and diffusion coefficient (or viscosity, as in the original fluid mechanical context) , the general form of Burgers' equation (also known as viscous Burgers' equation) in one space dimension is the dissipative system:
Added space-time noise forms a stochastic Burgers' equation[3]
This stochastic PDE is equivalent to the Kardar–Parisi–Zhang equation in a field upon substituting . But whereas Burgers' equation only applies in one spatial dimension, the Kardar–Parisi–Zhang equation generalises to multiple dimensions.
When the diffusion term is absent (i.e. d = 0), Burgers' equation becomes the inviscid Burgers' equation:
which is a prototype for conservation equations that can develop discontinuities (shock waves). The previous equation is the 'advection form' of the Burgers' equation. The 'conservation form' is
Solution
Inviscid Burgers' equation
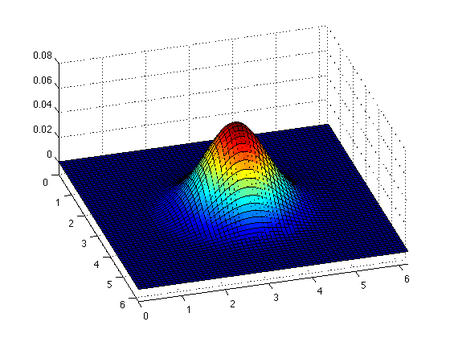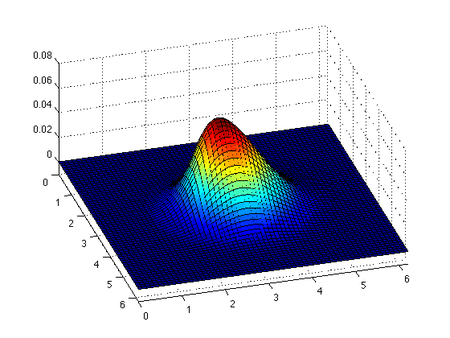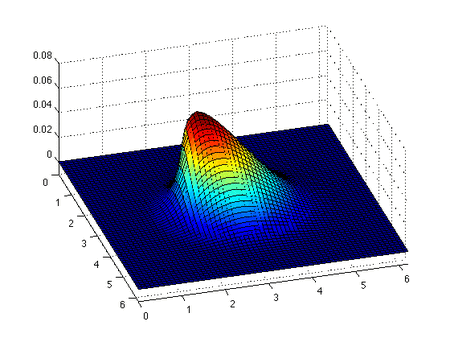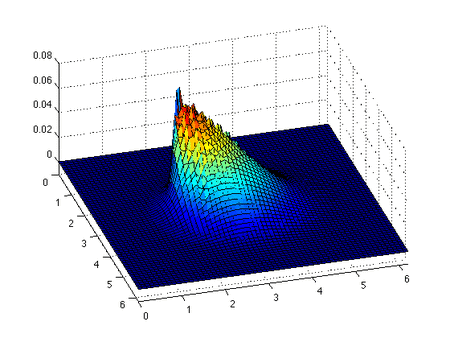
The inviscid Burgers' equation is a conservation equation, more generally a first order quasilinear hyperbolic equation. In fact by defining its current density as the kinetic energy density:
it can be put into the current density homogeneous form:
The solution of conservation equations can be constructed by the method of characteristics. This method yields that if is a solution of the ordinary differential equation
then is constant as a function of . For Burgers equation in particular is a solution of the system of ordinary equations:
The solutions of this system are given in terms of the initial values by
Substitute , then . Now the system becomes
Conclusion:
This is an implicit relation that determines the solution of the inviscid Burgers' equation provided characteristics don't intersect. If the characteristics do intersect, then a classical solution to the PDE does not exist.
Viscous Burgers' equation
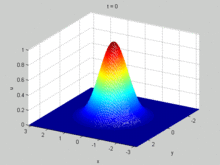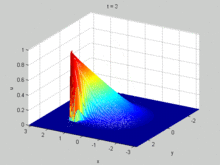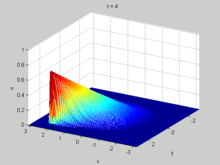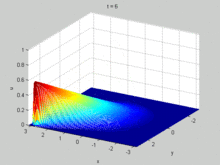
The viscous Burgers' equation can be linearized by the Cole–Hopf transformation [4]
which turns it into the equation
which can be integrated with respect to to obtain
where is a function that depends on boundary conditions. If identically (e.g. if the problem is to be solved on a periodic domain), then we get the diffusion equation
The diffusion equation can be solved, and the Cole-Hopf transformation inverted, to obtain the solution to the Burgers' equation:
Heat equation
Burgers' equation can notably be converted to a heat equation through a nonlinear substitution, as suggested by E. Hopf in 1950.[5] In fact substituting:
in Burgers' equation brings to:
that brings to:
where f(t) is an arbitrary function of time. With the transformation we can finally convert the latter to:
This is the searched heat equation, α being the diffusivity parameter. The initial condition is analogously transformed as:
where the fixed point of integration here is 0, but in general it can be set arbitrarily.
See also
References
- ↑ It relates to the Navier–Stokes momentum equation with the pressure term removed Burgers Equation (PDF): here the variable is the flow speed y=u
- ↑ It arises from Westervelt equation with an assumption of strictly forward propagating waves and the use of a coordinate transformation to a retarded time frame: here the variable is the pressure
- ↑ W. Wang and A. J. Roberts. Diffusion approximation for self-similarity of stochastic advection in Burgers’ equation. Communications in Mathematical Physics, July 2014.
- ↑ Eberhard Hopf (September 1950). "The partial differential equationy yt + yyx = μyxx". Communications on Pure and Applied Mathematics. 3 (3): 201–230. doi:10.1002/cpa.3160030302.
- ↑ Landau, Lifshits, 'Fluid Mechanics', par. 93, Problem 2
External links
- Burgers' Equation at EqWorld: The World of Mathematical Equations.
- Burgers' Equation at NEQwiki, the nonlinear equations encyclopedia.
- Burgers shock-waves and sound in a 2D microfluidic droplets ensemble Phys. Rev. Lett. 103, 114502 (2009).
- Burgers' Equation Wolfram|Alpha search results.