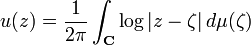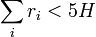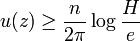Cartan's lemma (potential theory)

In potential theory, a branch of mathematics, Cartan's lemma, named after Henri Cartan, is a bound on the measure and complexity of the set on which a logarithmic Newtonian potential is small.

Statement of the lemma

The following statement can be found in Levin's book.^[1]

Let μ be a finite positive Borel measure on the complex plane C with μ(C) = n. Let u(z) be the logarithmic potential of μ:

$u(z) = \frac{1}{2\pi}\int_\mathbf{C} \log|z-\zeta|\,d\mu(\zeta)$

Given H ∈ (0, 1), there exist discs of radius r_i such that

$\sum_i r_i < 5H\,$

and

$u(z) \ge \frac{n}{2\pi}\log \frac{H}{e}$

for all z outside the union of these discs.

Notes

1. B.Ya. Levin, Lectures on Entire Functions