Catenoid

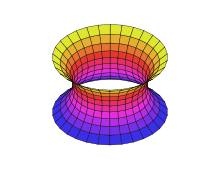
A catenoid

A catenoid obtained from the rotation of a catenary

A catenoid is a surface in 3-dimensional Euclidean space arising by rotating a catenary curve about its directrix (see animation on the right). Not counting the plane, it is the first non-trivial minimal surface to be discovered. It was found and proved to be minimal by Leonhard Euler in 1744.^[1]

Early work on the subject was published also by Jean Baptiste Meusnier.^[2] There are only two minimal surfaces of revolution (surfaces of revolution which are also minimal surfaces): the plane and the catenoid.^[3]

The catenoid may be defined by the following parametric equations:

$x=c\cosh {\frac {v}{c}}\cos u$

$y=c\cosh {\frac {v}{c}}\sin u$

$z=v$

where ${\displaystyle u\in [-\pi ,\pi )}$ and $v \in \mathbb{R}$ and $c$ is a non-zero real constant.

In cylindrical coordinates:

$\rho =c\cosh {\frac {z}{c}}$

where $c$ is a real constant.

A physical model of a catenoid can be formed by dipping two circles into a soap solution and slowly drawing the circles apart.

The catenoid may be also defined approximately by the Stretched grid method as a facet 3D model.

Helicoid transformation

Animation showing the deformation of a helicoid into a catenoid.

Because they are members of the same associate family of surfaces, one can bend a catenoid into a portion of a helicoid without stretching. In other words, one can make a (mostly) continuous and isometric deformation of a catenoid to a portion of the helicoid such that every member of the deformation family is minimal (having a mean curvature of zero). A parametrization of such a deformation is given by the system

$x(u,v)=\cos \theta \,\sinh v\,\sin u+\sin \theta \,\cosh v\,\cos u$

$y(u,v)=-\cos \theta \,\sinh v\,\cos u+\sin \theta \,\cosh v\,\sin u$

$z(u,v)=u\cos \theta +v\sin \theta \,$

for $(u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )$, with deformation parameter $-\pi <\theta \leq \pi$,

where $\theta =\pi$ corresponds to a right-handed helicoid, $\theta =\pm \pi /2$ corresponds to a catenoid, and $\theta =0$ corresponds to a left-handed helicoid.

Architecture

design of building igloos spiral

The Inuit learned to develop their igloo structures by implementing a catenary of revolution shape which offers optimal balance between height and diameter of the structure without risk of collapsing under the weight of compacted snow.^[4] This is slightly different from what is typically called a catenoid in that the catenary is rotated about its center, forming a surface with the topology of a bowl rather than that of a cylinder.

References

1. Eulero, Leonhardo (1952) [1744]. Carathëodory, ed. Methodus inveniendi lineas curvas : maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti [A method for finding the property of maxima or minima of curves and, as the sense of receiving, or Solution of isoperimetric problems in the broadest sense] (in Latin). 24 (MDCCXLIV ed.). Bernae: Orell Füssli Turici. ISBN 9783764314248. Archived from the original on archivedate. Retrieved 1 August 2015. Check date values in: |archive-date= (help)
2. Meusnier, J. B (1881). Mémoire sur la courbure des surfaces [Memory on the curvature of surfaces.] (PDF) (in French). Bruxelles: F. Hayez, Imprimeur De L'Acdemie Royale De Belgique. pp. 477–510. ISBN 9781147341744.
3. Catenoid at MathWorld
4. Handy, Richard L. (Dec 1973). "The Igloo and the Natural Bridge as Ultimate Structures" (PDF). Arctic. Arctic Institute of North America. 26 (4): 276–277. doi:10.14430/arctic2926.

External links

• Hazewinkel, Michiel, ed. (2001), "Catenoid", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
• Catenoid - WebGL model