Centered tree
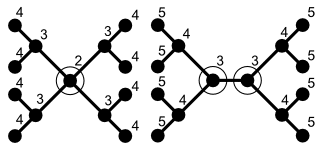
In discrete mathematics, a centered tree is a tree with only one center, and a bicentered tree is a tree with two centers.
Given a graph, the eccentricity of a vertex v is defined as the greatest distance from v to any other vertex. A center (also: centroid) of a graph is a vertex with minimal eccentricity. A graph can have an arbitrary number of centers. However, Jordan (1869) has proved that for trees, there are only two possibilities:
- The tree has precisely one center (centered trees).
- The tree has precisely two centers (bicentered trees). In this case, the two centers are adjacent.
A proof of this fact is given, for example, by Knuth.[1]
Notes
- ↑ (Knuth 1997), p. 387 and p. 589
References
- Jordan, Camille (1869). "Sur les assemblages de lignes". Journal für die reine und angewandte Mathematik (in French). 70 (2): 185–190.
- Knuth, Donald E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms (3rd ed.). Addison-Wesley Professional. ISBN 0-201-89683-4.
External links
This article is issued from Wikipedia - version of the 5/27/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.