Chomsky hierarchy

Within the fields of computer science and linguistics, specifically in the area of formal languages, the Chomsky hierarchy (occasionally referred to as Chomsky–Schützenberger hierarchy) is a containment hierarchy of classes of formal grammars. This hierarchy of grammars was described by Noam Chomsky in 1956.^[1] It is also named after Marcel-Paul Schützenberger, who played a crucial role in the development of the theory of formal languages.

Formal grammars

A formal grammar of this type consists of a finite set of production rules (left-hand side → right-hand side), where each side consists of a sequence of the following symbols:

• a finite set of nonterminal symbols (indicating that some production rule can yet be applied)
• a finite set of terminal symbols (indicating that no production rule can be applied)
• a start symbol (a distinguished nonterminal symbol)

A formal grammar defines (or generates) a formal language, which is a (usually infinite) set of finite-length sequences of symbols that may be constructed by applying production rules to another sequence of symbols (which initially contains just the start symbol). A rule may be applied by replacing an occurrence of the symbols on its left-hand side with those that appear on its right-hand side. A sequence of rule applications is called a derivation. Such a grammar defines the formal language: all words consisting solely of terminal symbols which can be reached by a derivation from the start symbol.

Nonterminals are often represented by uppercase letters, terminals by lowercase letters, and the start symbol by S. For example, the grammar with terminals {a, b}, nonterminals {S, A, B}, production rules

S → AB

S → ε (where ε is the empty string)

A → aS

B → b

and start symbol S, defines the language of all words of the form $a^n b^n$ (i.e. n copies of a followed by n copies of b).

The following is a simpler grammar that defines the same language: Terminals {a, b}, Nonterminals {S}, Start symbol S, Production rules

S → aSb

S → ε

As another example, a grammar for a toy subset of English language is given by:

terminals

{generate, hate, great, green, ideas, linguists}

nonterminals

{SENTENCE, NOUNPHRASE, VERBPHRASE, NOUN, VERB, ADJ}

production rules

SENTENCE → NOUNPHRASE VERBPHRASE

NOUNPHRASE → ADJ NOUNPHRASE

NOUNPHRASE → NOUN

VERBPHRASE → VERB NOUNPHRASE

VERBPHRASE → VERB

NOUN → ideas

NOUN → linguists

VERB → generate

VERB → hate

ADJ → great

ADJ → green

and start symbol SENTENCE. An example derivation is

SENTENCE → NOUNPHRASE VERBPHRASE → ADJ NOUNPHRASE VERBPHRASE → ADJ NOUN VERBPHRASE → ADJ NOUN VERB NOUNPHRASE → ADJ NOUN VERB ADJ NOUNPHRASE → ADJ NOUN VERB ADJ ADJ NOUNPHRASE → ADJ NOUN VERB ADJ ADJ NOUN → great NOUN VERB ADJ ADJ NOUN → great linguists VERB ADJ ADJ NOUN → great linguists generate ADJ ADJ NOUN → great linguists generate great ADJ NOUN → great linguists generate great green NOUN → great linguists generate great green ideas.

Other sequences that can be derived from this grammar are: "ideas hate great linguists", and "ideas generate". While these sentences are nonsensical, they are syntactically correct. A syntactically incorrect sentence ( e.g. "ideas ideas great hate") cannot be derived from this grammar. See "Colorless green ideas sleep furiously" for a similar example given by Chomsky in 1957; see Phrase structure grammar and Phrase structure rules for more natural language examples and the problems of formal grammar in that area.

The hierarchy

Set inclusions described by the Chomsky hierarchy

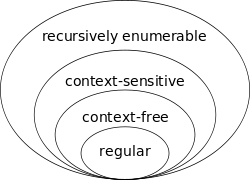
The Chomsky hierarchy consists of the following levels:

• Type-0 grammars (unrestricted grammars) include all formal grammars. They generate exactly all languages that can be recognized by a Turing machine. These languages are also known as the recursively enumerable or Turing-recognizable languages.^[2] Note that this is different from the recursive languages which can be decided by an always-halting Turing machine.
• Type-1 grammars (context-sensitive grammars) generate the context-sensitive languages (also known as Turing-decidable or simply decidable languages). These grammars have rules of the form $\alpha A\beta \rightarrow \alpha\gamma\beta$ with $A$ a nonterminal and $\alpha$, $\beta$ and $\gamma$ strings of terminals and/or nonterminals. The strings $\alpha$ and $\beta$ may be empty, but $\gamma$ must be nonempty. The rule $S \rightarrow \epsilon$ is allowed if $S$ does not appear on the right side of any rule. The languages described by these grammars are exactly all languages that can be recognized by a linear bounded automaton (a nondeterministic Turing machine whose tape is bounded by a constant times the length of the input.)
• Type-2 grammars (context-free grammars) generate the context-free languages. These are defined by rules of the form $A \rightarrow \gamma$ with $A$ a nonterminal and $\gamma$ a string of terminals and/or nonterminals. These languages are exactly all languages that can be recognized by a non-deterministic pushdown automaton. Context-free languages – or rather its subset of deterministic context-free language – are the theoretical basis for the phrase structure of most programming languages, though their syntax also includes context-sensitive name resolution due to declarations and scope. Often a subset of grammars are used to make parsing easier, such as by an LL parser.
• Type-3 grammars (regular grammars) generate the regular languages. Such a grammar restricts its rules to a single nonterminal on the left-hand side and a right-hand side consisting of a single terminal, possibly followed by a single nonterminal (right regular). Alternatively, the right-hand side of the grammar can consist of a single terminal, possibly preceded by a single nonterminal (left regular); these generate the same languages – however, if left-regular rules and right-regular rules are combined, the language need no longer be regular. The rule $S \rightarrow \epsilon$ is also allowed here if $S$ does not appear on the right side of any rule. These languages are exactly all languages that can be decided by a finite state automaton. Additionally, this family of formal languages can be obtained by regular expressions. Regular languages are commonly used to define search patterns and the lexical structure of programming languages.

Note that the set of grammars corresponding to recursive languages is not a member of this hierarchy; these would be properly between Type-0 and Type-1.

Every regular language is context-free, every context-free language (not containing the empty string) is context-sensitive, every context-sensitive language is recursive and every recursive language is recursively enumerable. These are all proper inclusions, meaning that there exist recursively enumerable languages which are not context-sensitive, context-sensitive languages which are not context-free and context-free languages which are not regular.

Summary

The following table summarizes each of Chomsky's four types of grammars, the class of language it generates, the type of automaton that recognizes it, and the form its rules must have.

Grammar	Languages	Automaton	Production rules (constraints)
Type-0	Recursively enumerable	Turing machine	$\alpha \rightarrow \beta$ (no restrictions)
Type-1	Context-sensitive	Linear-bounded non-deterministic Turing machine	$\alpha A \beta \rightarrow \alpha \gamma \beta$
Type-2	Context-free	Non-deterministic pushdown automaton	$A \rightarrow \gamma$
Type-3	Regular	Finite state automaton	$A \rightarrow a$ and $A \rightarrow aB$

There are further categories of formal languages, some of which are given in the expandable navigation box at the bottom of this page.

References

1. Chomsky, Noam (1956). "Three models for the description of language" (PDF). IRE Transactions on Information Theory (2): 113–124. doi:10.1109/TIT.1956.1056813.
2. Michael Sipser (1997). Introduction to the Theory of Computation 1st. Cengage Learning. ISBN 0-534-94728-X. The Church-Turing Thesis (Page 130)

• Chomsky, Noam (1959). "On certain formal properties of grammars" (PDF). Information and Control. 2 (2): 137–167. doi:10.1016/S0019-9958(59)90362-6.
• Chomsky, Noam; Schützenberger, Marcel P. (1963). "The algebraic theory of context free languages". In Braffort, P.; Hirschberg, D. Computer Programming and Formal Languages. Amsterdam: North Holland. pp. 118–161.
• Davis, Martin D.; Sigal, Ron; Weyuker, Elaine J. (1994). Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science (2nd ed.). Boston: Academic Press, Harcourt, Brace. p. 327. ISBN 0-12-206382-1.