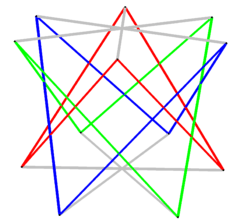
Compound of three tetrahedra
| Compound of 3 digonal antiprisms | |
|---|---|
 | |
| Type | Uniform compound |
| Uniform index | UC23 (n=3, p=2, q=1) |
| Polyhedra | 3 digonal antiprisms (tetrahedra) |
| Faces | 12 triangles |
| Edges | 24 |
| Vertices | 12 |
| Symmetry group | D6d, order 12 |
| Subgroup restricting to one constituent | D2d, order 4 |
In geometry, a compound of three tetrahedra can be constructed by three tetrahedra rotated by 60 degree turns along an axis of the middle of an edge. It has dihedral symmetry, D3d, order 12. It is a uniform prismatic compound of antiprisms, UC23.
It is similar to the compound of two tetrahedra with 90 degree turns. It has the same vertex arrangement as the convex hexagonal antiprism.
Related polytopes
A subset of edges of this compound polyhedron can generate a compound regular skew polygon, with 3 skew squares. Each tetrahedron contains one skew square. This regular compound polygon containing the same symmetry as the uniform polyhedral compound.
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.
External links
This article is issued from Wikipedia - version of the 3/20/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.