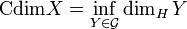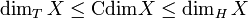Conformal dimension
In mathematics, the conformal dimension of a metric space X is the infimum of the Hausdorff dimension over the conformal gauge of X, that is, the class of all metric spaces quasisymmetric to X.[1]
Formal definition
Let X be a metric space and 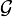 be the collection of all metric spaces that are quasisymmetric to X. The conformal dimension of X is defined as such
be the collection of all metric spaces that are quasisymmetric to X. The conformal dimension of X is defined as such
Properties
We have the following inequalities, for a metric space X:
The second inequality is true by definition. The first one is deduced from the fact that the topological dimension T is invariant by homeomorphism, and thus can be defined as the infimum of the Hausdorff dimension over all spaces homeomorphic to X.
Examples
- The conformal dimension of
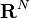 is N, since the topological and Hausdorff dimensions of Euclidean spaces agree.
is N, since the topological and Hausdorff dimensions of Euclidean spaces agree. - The Cantor set K is of null conformal dimension. However, there is no metric space quasisymmetric to K with a 0 Hausdorff dimension.
See also
References
- ↑ John M. Mackay, Jeremy T. Tyson, Conformal Dimension : Theory and Application, University Lecture Series, Vol. 54, 2010, Rhodes Island
This article is issued from Wikipedia - version of the 3/29/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.