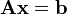Conjugate residual method
The conjugate residual method is an iterative numeric method used for solving systems of linear equations. It's a Krylov subspace method very similar to the much more popular conjugate gradient method, with similar construction and convergence properties.
This method is used to solve linear equations of the form
where A is an invertible and Hermitian matrix, and b is nonzero.
The conjugate residual method differs from the closely related conjugate gradient method primarily in that it involves more numerical operations and requires more storage, but the system matrix is only required to be Hermitian, not symmetric positive definite.
Given an (arbitrary) initial estimate of the solution 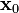 , the method is outlined below:
, the method is outlined below:
the iteration may be stopped once 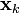 has been deemed converged. The only difference between this and the conjugate gradient method is the calculation of
has been deemed converged. The only difference between this and the conjugate gradient method is the calculation of 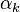 and
and 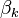 (plus the optional incremental calculation of
(plus the optional incremental calculation of 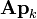 at the end).
at the end).
Note: the above algorithm can be transformed so to make only one symmetric matrix-vector multiplication in each iteration.
Preconditioning
By making a few substitutions and variable changes, a preconditioned conjugate residual method may be derived in the same way as done for the conjugate gradient method:
The preconditioner 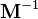 must be symmetric. Note that the residual vector here is different from the residual vector without preconditioning.
must be symmetric. Note that the residual vector here is different from the residual vector without preconditioning.
References
- Yousef Saad, Iterative methods for sparse linear systems (2nd ed.), page 194, SIAM. ISBN 978-0-89871-534-7.