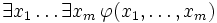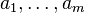Conservativity theorem
In mathematical logic, the conservativity theorem states the following: Suppose that a closed formula
is a theorem of a first-order theory 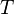 . Let
. Let 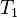 be a theory obtained from
be a theory obtained from 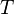 by extending its language with new constants
by extending its language with new constants
and adding a new axiom
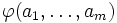 .
.
Then 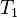 is a conservative extension of
is a conservative extension of 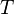 , which means that the theory
, which means that the theory 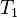 has the same set of theorems in the original language (i.e., without constants
has the same set of theorems in the original language (i.e., without constants 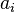 ) as the theory
) as the theory 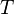 .
.
In a more general setting, the conservativity theorem is formulated for extensions of a first-order theory by introducing a new functional symbol:
- Suppose that a closed formula
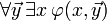 is a theorem of a first-order theory
is a theorem of a first-order theory 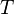 , where we denote
, where we denote 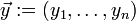 . Let
. Let 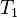 be a theory obtained from
be a theory obtained from 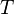 by extending its language with new functional symbol
by extending its language with new functional symbol 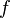 (of arity
(of arity 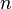 ) and adding a new axiom
) and adding a new axiom 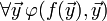 . Then
. Then 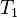 is a conservative extension of
is a conservative extension of 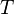 , i.e. the theories
, i.e. the theories 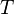 and
and 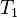 prove the same theorems not involving the functional symbol
prove the same theorems not involving the functional symbol 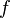 ).
).
References
- Elliott Mendelson (1997). Introduction to Mathematical Logic (4th ed.) Chapman & Hall.
- J.R. Shoenfield (1967). Mathematical Logic. Addison-Wesley Publishing Company.
This article is issued from Wikipedia - version of the 11/6/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.