Dimensional Fact Model

The Dimensional Fact Model (DFM)^[1] is an ad hoc and graphical formalism specifically devised to support the conceptual modeling phase in a DW project. DFM is extremely intuitive and can be used by analysts and non-technical users as well. A short-term working is sufficient to realize a clear and exhaustive representation of multidimensional concepts (e.g., attributes, measures and hierarchies). It can be used from the initial DW life-cycle steps, to rapidly devise a conceptual model to share with customers.

Data Warehouses (DWs) are databases used by decision makers to analyze the status and the development of an organization. DWs are based on large amounts of data integrated from heterogeneous sources into multidimensional databases, and they are optimized for accessing data in a way that comes naturally to human analysts (e.g., OLAP applications).

Data in a DW are organized according to the multidimensional model, that hinges on the concepts of fact (a focus of interest for the decision-making process, such as sales and orders) and dimension (a coordinate for analyzing a fact, such as time, customer, and product). Each fact is quantified through a set of numerical measures, such as the quantity of product sold, the price of products, etc.

DW design and development require ad hoc methodologies and an appropriate life-cycle.^[1]^[2]^[3]

Overview

The DFM is a graphical conceptual model, specifically devised for multidimensional design, in order to:

lend effective support to conceptual design
create an environment in which user queries may be formulated intuitively
make communication possible between designers and end users with the goal of formalizing requirement specifications
build a stable platform for logical design
provide clear and expressive design documentation.

The conceptual representation generated by the DFM consists of a set of fact schemata. Fact schemata model facts, measures, dimensions, and hierarchies (see Figure 1). Besides these basic elements, the DFM includes a large set of constructs for expressing the multitude of conceptual nuances that characterize actual modeling scenarios in projects of small to large complexity. A multidimensional schema modeled with the DFM can easily (i.e., semi-automatically) be implemented on both ROLAP and MOLAP platforms.

Basic concepts

A fact is a concept relevant to decision-making processes. It typically models a set of events taking place within a company. Examples of facts in the commercial domain are sales, shipments, purchases, and complaints.

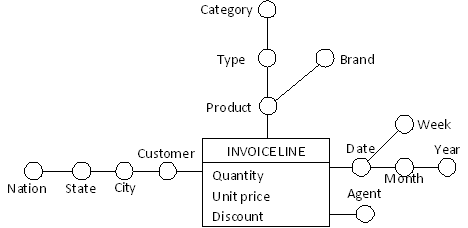
A measure is a numerical property of a fact and describes a quantitative attribute that is relevant to analysis. For example, each sale is measured by the number of units sold, the unit price, and the total receipts.

A dimension is a property, with a finite domain, that describes an analysis coordinate of the fact. A fact generally has multiple dimensions that define its minimum representation granularity. Typical dimensions for the sales fact are products, stores, and dates; in which case, the basic information that can be represented is product sales in one store in one day.

A fact is represented by a box that displays the fact name along with the measure names. Small circles represent the dimensions, which are linked to the fact by straight lines (see Figure 1).

A dimensional attribute is a property, with a finite domain, of a dimension. Like dimensions, a dimensional attribute is represented by a circle. For instance, a product may be described by its type, category, and brand; a customer may be represented by city and nation. The relationships among the dimensional attributes are expressed by hierarchies.

A hierarchy is a directed tree whose nodes are dimensional attributes and whose arcs model many-to-one associations between dimensional attribute pairs. A hierarchy includes a dimension, positioned at the tree’s root, and all of the dimensional attributes that describe it. Arcs are graphically represented by straight lines that connect dimensional attributes. Hierarchies define the way elemental business events can be selected and aggregated for decision-making processes.

Advanced concepts

A descriptive attribute specifies a property of a dimension attribute, to which it is related by a x-to-one association. Descriptive attributes cannot be used for aggregation; they are always leaves of a hierarchy and are graphically represented by horizontal lines, like Telephone number in Figure 2.

A cross-dimensional attribute is a dimensional or descriptive attribute whose value is defined by the combination of two or more dimensional attributes, possibly belonging to different hierarchies. For example, if a product value added tax (VAT) depends both on the product category and on the country where the product is sold, you can use a cross-dimensional attribute to represent it. Figure 2 shows this example by joining the arcs that define a product VAT with a circular arc.

A convergence takes place when two dimensional attributes within a hierarchy are connected by two or more alternative paths of many-to-one associations. Convergences are represented by letting two or more arcs reach the same dimensional attribute. For instance, in Figure 2 the geographic hierarchy on the customer dimension contains a convergence if we assume that, though no inclusion relationships exists between districts and cities/states, sales districts never cross the nation boundaries. In this case, each customer belongs to exactly one nation whichever of the two paths is followed.

Optional arcs are used to model scenarios for which an association represented in a fact schema is not defined for a subset of events. Optional arcs are marked with a dash. For instance, attribute diet in Figure 2 takes a value (such as cholesterol-free, gluten-free, or sugar-free) only for food products; for the other products, it is undefined.

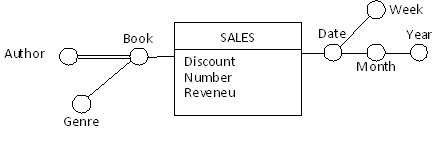
A multiple arc models a many-to-many association between the two dimensional attributes it connects. Graphically, it is denoted by doubling the line that represents the arc. Consider the fact schema modeling the sales of books, represented in Figure 3, whose dimensions are date and book. It would certainly be interesting to aggregate and select sales on the basis of book authors. However, it would not be accurate to model author as a dimensional child attribute of book because a book may have more than one author, and authors can write more than one book. Hence, the relationship between books and authors is modeled as a multiple arc.

References

1 2 Matteo Golfarelli and Stefano Rizzi. Data Warehouse Design - Modern Principles and Methodologies. McGrawHill, 2009.
↑ Ralph Kimball, et al. The Data Warehouse Lifecycle Toolkit. Wiley, 2008.
↑ Oscar Romero, Alberto Abelló. "A Survey of Multidimensional Modeling Methodologies". In Int. Journal on Data Warehousing and Mining (IJDWM), volume 5, number 2. Idea Group 2009. Pages 1-23. ISSN 1548-3924

This article is issued from Wikipedia - version of the 9/9/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.