Ditrigonal polyhedron
In geometry, there are seven uniform and uniform dual polyhedra named as ditrigonal.[1]
Ditrigonal vertex figures
There are five uniform ditrigonal polyhedra, all with icosahedral symmetry and 20 vertices.[1]
The three uniform star polyhedron with Wythoff symbol of the form 3 | p q or 3/2 | p q are ditrigonal, at least if p and q are not 2. Each polyhedron includes two types of faces, being of triangles, pentagons, or pentagrams. Their vertex configurations are of the form ababab with a symmetry of order 3. Here, term ditrigonal refers to a hexagon having a symmetry of order 3 (triangular symmetry) acting with 2 rotational orbits on the 6 angles of the vertex figure (The word "ditrigonal" means "having two sets of 3 angles").[2]
| Type | Small ditrigonal icosidodecahedron | Ditrigonal dodecadodecahedron | Great ditrigonal icosidodecahedron |
|---|---|---|---|
| Image |  |
 |
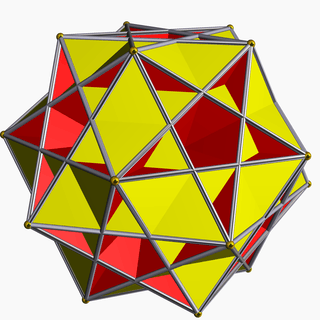 |
| Vertex figure |  |
 |
 |
| Vertex configuration | 3. 5⁄2.3. 5⁄2.3. 5⁄2 | 5. 5⁄3.5. 5⁄3.5. 5⁄3 | (3.5.3.5.3.5)/2 |
| Faces | 32 20 {3}, 12 { 5⁄2 } |
24 12 {5}, 12 { 5⁄2 } |
32 20 {3}, 12 {5} |
| Wythoff symbol | 3 | 5/2 3 | 3 | 5/3 5 | 3 | 3/2 5 |
| Coxeter diagram |
Other uniform ditrigonal polyhedra
The small ditrigonal dodecicosidodecahedron and the great ditrigonal dodecicosidodecahedron are also uniform.
Their duals are respectively the small ditrigonal dodecacronic hexecontahedron and great ditrigonal dodecacronic hexecontahedron.[1]
See also
References
Notes
- 1 2 3 Har'El, 1993
- ↑ Uniform Polyhedron, mathworld (retrieved 10 June 2016)
Bibliography
- Coxeter, H.S.M., M.S. Longuet-Higgins and J.C.P Miller, Uniform Polyhedra, Phil. Trans. 246 A (1954) pp. 401–450.
- Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57–110, 1993. Zvi Har’El, Kaleido software, Images, dual images
Further reading
- Johnson, N.; The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Skilling, J. (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 278: 111–135, doi:10.1098/rsta.1975.0022, ISSN 0080-4614, JSTOR 74475, MR 0365333