Dual object
In category theory, a branch of mathematics, it is possible to define a concept of dual object generalizing the concept of dual space in linear algebra.
A category in which each object has a dual is called autonomous or rigid.
Definition
Consider an object 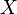 in a monoidal category
in a monoidal category 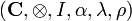 . The object
. The object 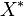 is called a left dual of
is called a left dual of 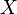 if there exist two morphsims
if there exist two morphsims
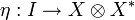 , called the coevaluation, and
, called the coevaluation, and 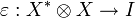 , called the evaluation,
, called the evaluation,
such that the following two diagrams commute
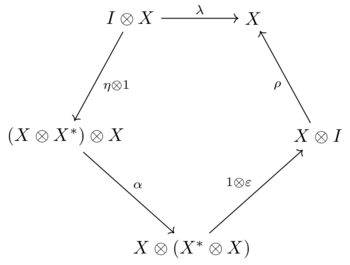 |
and |  |
The object 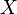 is called the right dual of
is called the right dual of 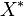 . Left duals are canonically isomorphic when they exist, as are right duals. When C is braided (or symmetric), every left dual is also a right dual, and vice versa.
. Left duals are canonically isomorphic when they exist, as are right duals. When C is braided (or symmetric), every left dual is also a right dual, and vice versa.
If we consider a monoidal category as a bicategory with one object, a dual pair is exactly an adjoint pair.
Categories with duals
A monoidal category where every object has a left (resp. right) dual is sometimes called a left (resp. right) autonomous category. Algebraic geometers call it a left (resp. right) rigid category. A monoidal category where every object has both a left and a right dual is called an autonomous category. An autonomous category that is also symmetric is called a compact closed category.
See also
References
- Peter Freyd and David Yetter (1989). "Braided Compact Closed Categories with Applications to Low-Dimensional Topology". Advances in Mathematics 77 (2): 156–182. doi:10.1016/0001-8708(89)90018-2.
- André Joyal and Ross Street. "The Geometry of Tensor calculus II". Synthese Lib 259: 29–68.