Electron optics

Magnetic lens

Electron optics is a mathematical framework for the calculation of particle paths along given electrostatic or magnetostatic fields. The term optics is used because a charged particle beam can be manipulated using magnetic or electrostatic lenses in a similar fashion to the manipulation of a light beam with optical lenses.

Electron optics calculations are, besides other uses, needed for electron microscopes and are also crucial for the design of modern particle accelerators. In paraxial approximation, the calculations can be done using ray transfer matrix analysis.

An einzel lens, a specific type of electrostatic lens. This figure shows the electron path. Six plates are parallel to the flight path with the middle plate at a particular potential. (This diagram was made for positive ions, and shows a positive voltage on the central plate. For electrons this voltage must be negative.)

Electron properties

Main article: Electron

Electrons are charged particles (point charges with rest mass). The electron also has an associated spin of + 1/2. While in motion an electron possesses kinetic energy, regardless of any imposed charge field—this could be achieved by accelerating electrons via a voltage differential into a screened "field-free" region, which initially imparts the energy required to accelerate the electron. Given sufficient voltage, the electron can be accelerated sufficiently fast to exhibit measurable relativistic effects, and the velocity must be accounted for relativistically. According to the wave particle duality, electrons can also be considered as wave propagations and therefore have associated wave properties such as wavelength, phase and amplitude.

With respect to electron optics, the nature of the electron as a charged particle causes electrons to interact with imposed electron fields, and their spin causes magnetic field interactions as well. These interactions form the fundamentals of electron optical theory.

Field interactions

Particle interpretation

Magnetic fields interact with an electron in a manner that alters velocity independently of kinetic energy (velocity magnitude). Electrons move according to the cross product of the magnetic field and the electron propagation vector, such that, in an infinite uniform field moving electrons take a circular motion at a constant radius dependent upon electron velocity and field strength according to the following equation, which can be derived from circular motion:

r={\frac {2mcv}{eH}}

where r is the orbit radius, m is the mass of an electron, v is the electron velocity, e is the charge on the electron and H is the applied magnetic field. Electrons that have a velocity component that is parallel to the magnetic field will rather "stretch out" the circle and form helical paths, the pitch of which is subject to the rotation period and the parallel velocity component.

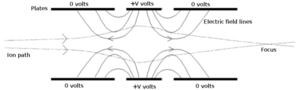
In the case of an applied electrostatic field, an electron will deflect towards the positive gradient of the field. Notably, this crossing of electrostatic field lines means that electrons, as they move through electrostatic fields change the magnitude of their velocity, whereas in magnetic fields, only the velocity direction is modified.

As electrons can exhibit non-particle (wave-like) effects such as diffraction, a full analysis of electron paths can be obtained by solving Maxwell's equation—however in many situations, the particle interpretation may provide a sufficient approximation with great reduction in complexity.

One further property of electrons is that they interact strongly with matter as they are sensitive to not only the nucleus, but also the matter's electron charge cloud. Therefore, electrons require vacuum to propagate any reasonable distance, such as would be desirable in electron optic system.

Penetration in vacuum is dictated by mean free path, a measure of the probability of collision between electrons and matter, approximate values for which can be derived from Poisson statistics.

Quantum theory

Although not very common, it is also possible to derive effects of magnetic structures to charged particles starting from the Dirac equation.^[1]

References

↑ Jagannathan, R.; Simon, R.; Sudarshan, E. C. G.; Mukunda, N. (1989). "Quantum theory of magnetic electron lenses based on the Dirac equation". Physics Letters A. 134 (8–9): 457. Bibcode:1989PhLA..134..457J. doi:10.1016/0375-9601(89)90685-3.

Air Force Research Laboratory - Electron Optics Program

This article is issued from Wikipedia - version of the 10/6/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.