Elongated bicupola
| Set of elongated bicupolae | |
|---|---|
|
Example pentagonal ortho form | |
| Faces |
2n triangles 4n squares 2 n-gon |
| Edges | 12n |
| Vertices | 6n |
| Symmetry group |
Ortho: Dnh, [2,n], (*n22), order 4n Gyro: Dnd, [2+,2n], (2*n), order 4n |
| Properties | convex |
In geometry, the elongated bicupolae are two infinite sets of polyhedra, constructed by adjoining two n-gonal cupolas to an n-gonal prism. They have 2n triangles, 4n squares, and 2 n-gon. The ortho forms have the cupola aligned, while gyro forms are counter aligned.
| 3 | 4 | 5 |
|---|---|---|
| Elongated orthobicupola | ||
| J35 | Semiregular | J38 |
| Elongated triangular orthobicupola | Elongated square orthobicupola (rhombicuboctahedron) |
Elongated pentagonal orthobicupola |
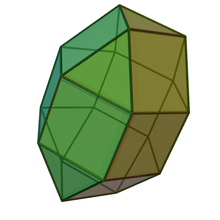 |
 |
 |
 |
 |
 |
| Elongated gyrobicupola | ||
| J36 | J37 | J39 |
| Elongated triangular gyrobicupola | Elongated square gyrobicupola (pseudorhombicuboctahedron) |
Elongated pentagonal gyrobicupola |
 |
 |
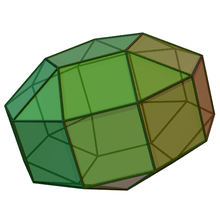 |
 |
 |
 |
See also
References
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
This article is issued from Wikipedia - version of the 2/20/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.