Fast Walsh–Hadamard transform

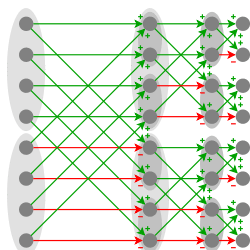
The fast Walsh–Hadamard transform applied to a vector of length 8

Example for the input vector (1,0,1,0,0,1,1,0)

In computational mathematics, the Hadamard ordered fast Walsh–Hadamard transform (FWHT_h) is an efficient algorithm to compute the Walsh–Hadamard transform (WHT). A naive implementation of the WHT would have a computational complexity of O($N^{2}$). The FWHT_h requires only $N\log N$ additions or subtractions.

The FWHT_h is a divide and conquer algorithm that recursively breaks down a WHT of size $N$ into two smaller WHTs of size $N/2$. This implementation follows the recursive definition of the $2N\times 2N$ Hadamard matrix $H_{N}$:

$H_{N}={\frac {1}{\sqrt {2}}}{\begin{pmatrix}H_{N-1}&H_{N-1}\\H_{N-1}&-H_{N-1}\end{pmatrix}}.$

The $1/{\sqrt {2}}$ normalization factors for each stage may be grouped together or even omitted.

The sequency ordered, also known as Walsh ordered, fast Walsh–Hadamard transform, FWHT_w, is obtained by computing the FWHT_h as above, and then rearranging the outputs.

See also

• Fast Fourier transform

References

• Fino, B. J.; Algazi, V. R. (1976). "Unified Matrix Treatment of the Fast Walsh–Hadamard Transform". IEEE Transactions on Computers. 25 (11): 1142–1146. doi:10.1109/TC.1976.1674569.

External links

• Charles Constantine Gumas,