Fatou–Bieberbach domain
In mathematics, a Fatou–Bieberbach domain is a proper subdomain of 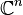 , biholomorphically equivalent to
, biholomorphically equivalent to 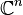 . That is, an open set
. That is, an open set 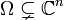 is called a Fatou–Bieberbach domain if there exists a bijective holomorphic function
is called a Fatou–Bieberbach domain if there exists a bijective holomorphic function 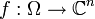 whose inverse function
whose inverse function 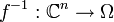 is holomorphic.
is holomorphic.
History
As a consequence of the Riemann mapping theorem, there are no Fatou–Bieberbach domains in the case n = 1. Pierre Fatou and Ludwig Bieberbach first explored such domains in higher dimensions in the 1920s, hence the name given to them later. Since the 1980s, Fatou–Bieberbach domains have again become the subject of mathematical research.
References
- Fatou, Pierre: "Sur les fonctions méromorphes de deux variables. Sur certains fonctions uniformes de deux variables." C.R. Paris 175 (1922)
- Bieberbach, Ludwig: "Beispiel zweier ganzer Funktionen zweier komplexer Variablen, welche eine schlichte volumtreue Abbildung des
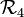 auf einen Teil seiner selbst vermitteln". Preussische Akademie der Wissenschaften. Sitzungsberichte (1933)
auf einen Teil seiner selbst vermitteln". Preussische Akademie der Wissenschaften. Sitzungsberichte (1933) - Rosay, J.-P. and Rudin, W: "Holomorphic maps from
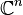 to
to 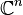 ". Trans. A.M.S. 310 (1988)
". Trans. A.M.S. 310 (1988)
This article is issued from Wikipedia - version of the 5/25/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.