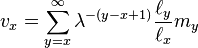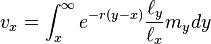Reproductive value (population genetics)

Reproductive value (not to be confused with breeding value) is a concept in demography and population genetics that represents the discounted number of future girl children that will be born to a woman of a specific age. Ronald Fisher first defined reproductive value in his 1930 book The Genetical Theory of Natural Selection where he proposed that future offspring be discounted at the rate of growth of the population; this implies that sexually reproductive value measures the contribution of an individual of a given age to the future growth of the population.[1][2]
Definition
Consider a species with a life history table with survival and reproductive parameters given by 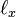 and
and  , where
, where
-
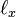 = probability of surviving from age 0 to age
= probability of surviving from age 0 to age 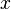
and
-
 = average number of offspring produced by an individual of age
= average number of offspring produced by an individual of age 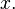
In a population with a discrete set of age classes, Fisher's reproductive value is calculated as
where 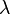 is the long-term population growth rate given by the dominant eigenvalue of the Leslie matrix. When age classes are continuous,
is the long-term population growth rate given by the dominant eigenvalue of the Leslie matrix. When age classes are continuous,
where  is the intrinsic rate of increase or Malthusian growth rate.
is the intrinsic rate of increase or Malthusian growth rate.
See also
Notes
- Fisher, R. A. 1930. The Genetical Theory of Natural Selection. Oxford University Press, Oxford.
- Keyfitz, N. and Caswell, H. 2005. Applied Mathematical Demography. Springer, New York. 3rd edition. doi:10.1007/b139042
References
- ↑ A theory of Fisher's reproductive value Published by PubMed.gov
- ↑ The Relation Between Reproductive Value and Genetic Contribution Published by the Genetics journal