Fixed-point space

In mathematics, a Hausdorff space X is called a fixed-point space if every continuous function 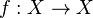$f:X\rightarrow X$ has a fixed point.

For example, any closed interval [a,b] in 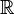$\mathbb R$ is a fixed point space, and it can be proved from the intermediate value property of real continuous function. The open interval (a, b), however, is not a fixed point space. To see it, consider the function 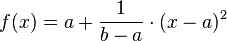$f(x) = a + \frac{1}{b-a}\cdot(x-a)^2$, for example.

Any linearly ordered space that is connected and has a top and a bottom element is a fixed point space.

Note that, in the definition, we could easily have disposed of the condition that the space is Hausdorff.

References

• Vasile I. Istratescu, Fixed Point Theory, An Introduction, D. Reidel, the Netherlands (1981). ISBN 90-277-1224-7
• Andrzej Granas and James Dugundji, Fixed Point Theory (2003) Springer-Verlag, New York, ISBN 0-387-00173-5
• William A. Kirk and Brailey Sims, Handbook of Metric Fixed Point Theory (2001), Kluwer Academic, London ISBN 0-7923-7073-2