Flow through cascades

A flow through cascade is a row of blades representing the blade ring of a turbo machine.^[1] These blades can be arranged in straight line or annular, thus representing an actual blade row, these arrangements are known as “rectilinear cascade” and “annular cascade” respectively. The “annular cascade” is more towards a real-life situation. The above arrangements are employed for the cascades of axial-flow turbo machines, but when the flow through the ring of blades is in the radial direction (inward or outward), the arrangement is termed as a “radial cascade”.

Testing

For simulation of actual condition cascade of blades are tested in annular form in wind tunnel, and as in rotating device it is difficult to appreciate flow physics generally straight cascade or cascade tunnel is used for testing. As a result it reduces mechanical complication and interpretation of test results get simplifies in 2-D flow conditions.^[2]

Two Dimensional Flow

Fig 1.Two dimensional flow through a cascade

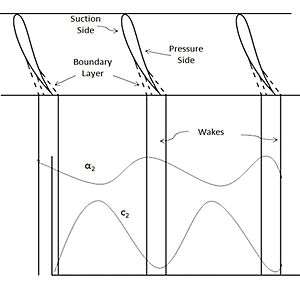
Due to rotation and boundary layer formation, flows in actual turbo machine is three dimensional. Assuming the flow to be two dimensional makes our problem quite easy. To do so we neglect the blade height. In axial machines flow is assumed to be two dimensional flow.In layman language three dimensional flow is reduced to two dimensional plane flow in which variations occur only in pitchwise and streamwise directions only. The boundary layer growth on the suction and pressure sides of the blades in a real flow leads to the formation of low energy regions in the exit flow field.The velocity ($c_{2}$) and angle (direction α₂) profiles at the exit of a cascade with two-dimensional flow are shown in Fig. 1. In two-dimensional flow these profiles remain constant at all blade heights.

Cascade Of Blades

Blades of a desired size and shape are assembled in a straight line or annular according to the cascade required. For assembling the blades, pitch(s) and stagger angle (γ). is defined. Blades of equal lengths are used in constructing a cascade. Blades for a cascade can be manufactured from wood, epoxy resin, glass wool, araldite or aluminium. Sometimes blades are made hollow to reduce the quantity of material and the weight of the blade. Generally, seven blades are used for cascade construction. The assembly is then fixed on the test section of the wind tunnel. Air at STP is blown over the cascade of blades to simulate the flow over an actual blade row in a turbo machine.

Measurement Of Static Pressure Distribution

Fig 2. Instrumented Blade

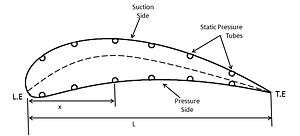
Fig 2 shows the instrumented blade which shows the hypodermic tubes which are closed at one end and runs through the whole length of the blade. They are present on both sides of the blade surface. Open end of the tubes is projected through the side walls and is used to transmit the local static pressure to the manometer.

Cascade Performance

The main aim of cascade is to deflect the flow at desired angles. The deflection depends on the exit angles for a fixed entry angle and the exit varies with change in the pitch.^[3][4][5] The deflection occurs due to loss in stagnation pressure and increase in entropy and this is irreversible in nature.
The performance of a blade row (cascade) can be obtained by measuring the exit air angle (α₂) and stagnation pressure loss (Δp₀) across it. Due to two –dimensional flow variation of exit air angle α₂ and Δp₀ variation in the tangential direction, has to be taken into account. This is done by averaging the mass over the length of a blade in the tangential direction.

The mass flow rate through this elemental distance dy of unit length is

${\displaystyle d{\dot {m}}=\rho c_{x}dy}$

Mass-flow rate over one blade pitch

${\displaystyle {\dot {m}}=\int \rho c_{x}dy}$

Tangential momentum of outgoing jet c_x2

${\displaystyle M_{y}=\int c_{y}d{\dot {m}}}$

Similarly,

${\displaystyle M_{x}=\int \rho c_{x2}dy}$

The mean value of the exit air angle of the cascade is obtained from Eqs

${\displaystyle \tan \alpha ={\frac {M_{y}}{M_{x}}}}$

The integrated value of the stagnation pressure loss is

${\displaystyle \Delta p_{0}={\frac {p_{01}-p_{02}}{d{\dot {m}}}}}$

Velocity Triangles

Fig 3. Inlet, outlet and mean velocity triangles, and blade forces(turbine blades)

Fig 3 shows the inlet,outlet and mean velocity triangles along with blade forces in a cascade. The velocity vectors c₁ and c₂ at the entry and exit are at air angles α₁ and α₂ respectively.

A mean velocity triangle for the flow through the cascade is defined by the following quantities

${\displaystyle C_{xm}=0.5(c_{x1}+c_{x2})}$

${\displaystyle C_{ym}=0.5(c_{y2}-c_{y1})}$

${\displaystyle \tan \alpha ={\frac {C_{ym}}{C_{xm}}}}$

For constant axial velocity,

${\displaystyle \tan \alpha _{m}=0.5(\tan \alpha _{2}-\tan \alpha _{1})}$

Blade Forces

The lift and the drag forces are perpendicular and parallel to the direction of the mean velocity $c_{m}$ respectively as shown in Fig. 3. The resultant of both the forces is the force F_r .This force is further resolved in axial and tangential directions F_x and F_y respectively. The main aim is to reduce the axial thrust and pressure losses δp₀ and maximise the tangential component on the cascade.

Tangential Forces

The tangential force on the blade is equal to the rate of change of momentum in the tangential direction. Using Fig 3, the following relation is obtained

${\displaystyle F_{y}=0.5(\rho l(c_{xm})^{2})2({\frac {s}{l}})(\tan \alpha _{1}+\tan \alpha _{2})}$

Axial Forces

The axial force takes place due to both the pressure difference and change of momentum in the axial direction. Using fig 3,the following relation is obtained

${\displaystyle F_{x}=(0.5\rho l(c_{2})^{2})({\frac {s}{l}})\cos ^{2}\alpha _{2}(\tan ^{2}\alpha _{2}-\tan ^{2}\alpha _{1})+s\Delta p_{0}}$

Lift forces

Lift force L acts in the direction perpendicular to c_m.The magnitude of lift force can be obtained by resolving the forces in velocity triangles in the direction of lift (Fig. 3), It is given by,

${\displaystyle L=(0.5\rho l(c_{m})^{2})2({\frac {s}{l}})\cos \alpha _{m}(\tan \alpha _{2}+\tan \alpha _{1})+s\Delta p_{0}\sin \alpha _{m}}$

Drag Forces

The drag force D is in the direction of cm and is obtained by resolving forces in its direction

${\displaystyle D=s\Delta p_{0}\cos \alpha _{m}}$

Losses

Losses in cascade occurs due to the three dimensional flow and the growth and separation of boundary layers that takes place on the surface of the blades. Other takes place due to the loss of stagnation pressure across the cascade and due to wasteful circulatory flows and the formation of shock waves.^[6][7]

Fig 4. Flow through tip clearance in a compressor cascade

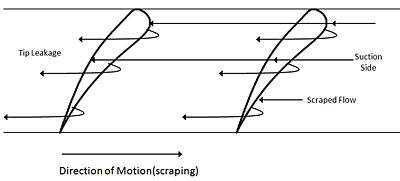
Various types of losses are mentioned below

Profile Losses

It is the total loss in stagnation pressure across the blade row divided by the difference between the stagnation pressure and the static pressure at the outlet. It takes place due to the formation of boundary layer which steepens due to adverse pressure gradient.

Secondary Losses

It arises due to three dimensional flows near the end walls. The term secondary losses occurs due to the three-dimensional vortical flow structures that develop in blade passages due to high turning of the flow and nonuniform inlet total pressure profiles. Flow which is transverse to the primary flow direction is termed as secondary flow. The boundary layer flow along the endwall contains spanwise velocity gradients^[8][9]

Tip Clearance losses

Tip clearance flow is created by the fluid that passes through the radial gap between the tips of the rotor blades and the stationary rotor casing. About one third of the losses of a high-pressure stage can be due to the tip clearance flow, which deteriorates the aerodynamic and thermal performance of the axial flow turbine

See also

• Effects of mach number and shock losses in turbomachines

References

1. "Elementary Cascade Theory and Gas Turbine Performance".
2. Yahya ,S.M, ”Turbine, Compressors & Fans”,4TH ED.McGraw Hill,2011,Chapter 8.
3. Balje, O.E., ‘‘Axial cascade technology and application to flow path designs’’, ASME J. Eng. Power, Vol 90, Series A, No. 4, Oct 1968.
4. Keast, F.H, “High speed cascade testing techniques”, Trans ASME, 74 ,685, 1952.
5. Lewis, R.I., “Annular cascade wind tunnel”, Engineer,215,341,London,1963.
6. Horlock , J.H., ”Losses and efficiencies in axial-flow turbines”, Int. J. Mech. Sci., 2, 1960..
7. Came, P.M., “Secondary loss measurements in a cascade in turbine blades”, Proc. Instn. Mech. Engrs., London, Conference Publication, 3,1973.
8. Belik, L., “Secondary flows in blade cascades of axial turbomachines and the possibility of reducing its unfavourable effects”, Int. JSME symposium on fluid machinery and fluidics, Tokyo, Sept. 1972.
9. Dunham,J., ‘A review of cascade data on secondary losses in turbines’, J. Mech. Eng. Sci., Vol. 12,1970.