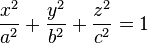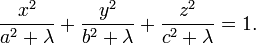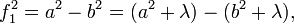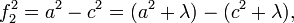Focaloid

Focaloid in 3D

In geometry, a focaloid is a shell bounded by two concentric, confocal ellipses (in 2D) or ellipsoids (in 3D). When the thickness of the shell becomes negligible, it is called a thin focaloid.

Mathematical definition (3D)

If one boundary surface is given by

$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$

with semiaxes a, b, c the second surface is given by

$\frac{x^2}{a^2+\lambda}+\frac{y^2}{b^2+\lambda}+\frac{z^2}{c^2+\lambda}=1.$

The thin focaloid is then given by the limit 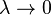$\lambda \to 0$.

In general, a focaloid could be understood as a shell consisting out of two closed coordinate surfaces of a confocal ellipsoidal coordinate system.

Confocal

Confocal ellipsoids share the same foci, which are given for the example above by

$f_1^2=a^2-b^2=(a^2+\lambda)-(b^2+\lambda), \,$

$f_2^2=a^2-c^2=(a^2+\lambda)-(c^2+\lambda), \,$

$f_3^2=b^2-c^2=(b^2+\lambda)-(c^2+\lambda).$

Physical meaning

A focaloid can be used as a construction element of a matter or charge distribution. The particular importance of focaloids lies in the fact that two different but confocal focaloids of the same mass or charge produce the same action on a test mass or charge in the exterior region.

See also

• Homoeoid

References

• Subrahmanyan Chandrasekhar (1969): Ellipsoidal Figures of Equilibrium. Yale University Press, London, Connecticut
• Routh, E. J.: A Treatise on Analytical Statics, Vol II, Cambridge University Press, Cambridge (1882).