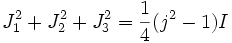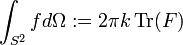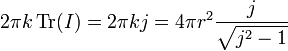Fuzzy sphere

In mathematics, the fuzzy sphere is one of the simplest and most canonical examples of non-commutative geometry. Ordinarily, the functions defined on a sphere form a commuting algebra. A fuzzy sphere differs from an ordinary sphere because the algebra of functions on it is not commutative. It is generated by spherical harmonics whose spin l is at most equal to some j. The terms in the product of two spherical harmonics that involve spherical harmonics with spin exceeding j are simply omitted in the product. This truncation replaces an infinite-dimensional commutative algebra by a 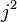$j^2$-dimensional non-commutative algebra.

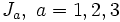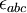The simplest way to see this sphere is to realize this truncated algebra of functions as a matrix algebra on some finite-dimensional vector space. Take the three j-dimensional matrices $J_a,~ a=1,2,3$ that form a basis for the j dimensional irreducible representation of the Lie algebra SU(2). They satisfy the relations $[J_a,J_b]=i\epsilon_{abc}J_c$, where $\epsilon_{abc}$ is the totally antisymmetric symbol with 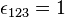$\epsilon_{123}=1$, and generate via the matrix product the algebra 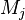$M_j$ of j dimensional matrices. The value of the SU(2) Casimir operator in this representation is

$J_1^2+J_2^2+J_3^2=\frac{1}{4}(j^2-1)I$

where I is the j-dimensional identity matrix. Thus, if we define the 'coordinates' 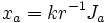$x_a=kr^{-1}J_a$ where r is the radius of the sphere and k is a parameter, related to r and j by 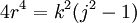$4r^4=k^2(j^2-1)$, then the above equation concerning the Casimir operator can be rewritten as

$x_1^2+x_2^2+x_3^2=r^2$,

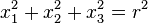which is the usual relation for the coordinates on a sphere of radius r embedded in three dimensional space.

One can define an integral on this space, by

$\int_{S^2}fd\Omega:=2\pi k \, \text{Tr}(F)$

where F is the matrix corresponding to the function f. For example, the integral of unity, which gives the surface of the sphere in the commutative case is here equal to

$2\pi k \, \text{Tr}(I)=2\pi k j =4\pi r^2\frac{j}{\sqrt{j^2-1}}$

which converges to the value of the surface of the sphere if one takes j to infinity.

See also

• Fuzzy torus

Notes

• Jens Hoppe, "Membranes and Matrix Models", lectures presented during the summer school on ‘Quantum Field Theory – from a Hamiltonian Point of View’, August 2–9, 2000, arXiv:hep-th/0206192
• John Madore, An introduction to Noncommutative Differential Geometry and its Physical Applications, London Mathematical Society Lecture Note Series. 257, Cambridge University Press 2002

References

J. Hoppe, Quantum Theory of a Massless Relativistic Surface and a Two dimensional Bound State Problem. PhD thesis, Massachusetts Institute of Technology, 1982.