Geometric tomography
Geometric tomography is a mathematical field that focuses on problems of reconstructing homogeneous (often convex) objects from tomographic data (this might be X-rays, projections, sections, brightness functions, or covariograms). More precisely, according to R.J. Gardner (who introduced the term), "Geometric tomography deals with the retrieval of information about a geometric object from data concerning its projections (shadows) on planes or cross-sections by planes."[1]
Theory
A key theorem in this area states that any convex body in 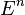 can be determined by parallel, coplanar
X-rays in a set of four directions whose slopes have a transcendental cross ratio.
can be determined by parallel, coplanar
X-rays in a set of four directions whose slopes have a transcendental cross ratio.
Examples
- Radon transform
- Funk transform (a.k.a. spherical Radon transform)
See also
References
- ↑ Gardner, R.J., Geometric Tomography, Cambridge University Press, Cambridge, UK, 2nd ed., 2006
External links
This article is issued from Wikipedia - version of the 12/22/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.