Graph C*-algebra
In mathematics, particularly the theory of C*-algebras, a graph C*-algebra is a universal C*-algebra associated to a directed graph. They form a rich class of C*-algebras encompassing Cuntz algebras, Cuntz-Krieger algebras, the Toeplitz algebra, etc. Also every AF-algebra is Morita equivalent[1] to a graph C*-algebra. As the structure of graph C*-algebras is fairly tractable with computable invariants, they play an important part in the classification theory of C*-algebras.
Definition
Let 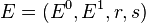 be a directed graph with a countable set of vertices
be a directed graph with a countable set of vertices 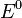 , a countable set of edges
, a countable set of edges 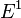 , and maps
, and maps 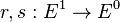 identifying the range and source of each edge, respectively. The graph C*-algebra corresponding to
identifying the range and source of each edge, respectively. The graph C*-algebra corresponding to 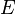 , denoted by
, denoted by 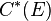 , is the universal C*-algebra generated by mutually orthogonal projections
, is the universal C*-algebra generated by mutually orthogonal projections 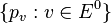 and partial isometries
and partial isometries 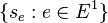 with mutually orthogonal ranges such that :
with mutually orthogonal ranges such that :
(i) 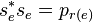 for all
for all 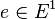
(ii) 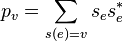 whenever
whenever 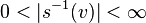
(iii) 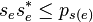 for all
for all 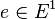 .
.
Examples of graph C*-algebras
| Directed graph (E) | Graph C*-algebra (C*(E)) |
|---|---|
| | 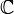 - the set of complex numbers - the set of complex numbers |
| | 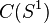 - the set of complex-valued continuous functions on the circle - the set of complex-valued continuous functions on the circle |
| | 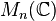 - the set of n x n matrices over - the set of n x n matrices over 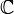 |
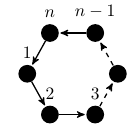 | 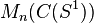 - the set of n x n matrices over - the set of n x n matrices over 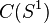 |
| |  - the set of compact operators over a separable Hilbert space - the set of compact operators over a separable Hilbert space |
| |  - Toeplitz algebra - Toeplitz algebra |
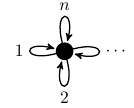 | 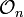 - Cuntz algebra - Cuntz algebra |
Notes
- ↑ D. Drinen,Viewing AF-algebras as graph algebras, Proc. Amer. Math. Soc., 128 (2000), pp. 1991–2000.