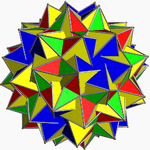
Great snub dodecicosidodecahedron
| Great snub dodecicosidodecahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 104, E = 180 V = 60 (χ = −16) |
| Faces by sides | (20+60){3}+(12+12){5/2} |
| Wythoff symbol | | 5/3 5/2 3 |
| Symmetry group | I, [5,3]+, 532 |
| Index references | U64, C80, W115 |
| Dual polyhedron | Great hexagonal hexecontahedron |
| Vertex figure |  3.3.3.5/2.3.5/3 |
| Bowers acronym | Gisdid |
In geometry, the great snub dodecicosidodecahedron is a nonconvex uniform polyhedron, indexed as U64. It has Coxeter diagram, 
and Schlaefli symbol s{(5/3,5/2,3)}. It has the unusual feature that its 24 pentagram faces occur in 12 coplanar pairs.
Related polyhedra
It shares its vertices and edges, as well as 20 of its triangular faces and all its pentagrammic faces, with the great dirhombicosidodecahedron, (although the latter has 60 edges not contained in the great snub dodecicosidodecahedron). It shares its other 60 triangular faces (and its pentagrammic faces again) with the great disnub dirhombidodecahedron.
The edges and triangular faces also occur in the compound of twenty octahedra. In addition, 20 of the triangular faces occur in one enantiomer of the compound of twenty tetrahemihexahedra, and the other 60 triangular faces occur in the other enantiomer.
 Convex hull |
Great snub dodecicosidodecahedron |
 Great dirhombicosidodecahedron |
 Great disnub dirhombidodecahedron |
 Compound of twenty octahedra |
 Compound of twenty tetrahemihexahedra |
Filling
There is some controversy on how to colour the faces of this polyhedron. Although the common way to fill in a polygon is to just colour its whole interior, this can result in some filled regions hanging as membranes over empty space. Hence, the "neo filling" is sometimes used instead as a more accurate filling. In the neo filling, orientable polyhedra are filled traditionally, but non-orientable polyhedra have their faces filled with the modulo-2 method (only odd-density regions are filled in). In addition, overlapping regions of coplanar faces can cancel each other out. The difference between the fillings of this polyhedron is very slight, but still present.[1]
Traditional filling |
 "Neo filling" |