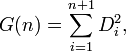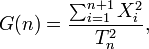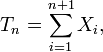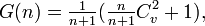Greenwood statistic
The Greenwood statistic is a spacing statistic and can be used to evaluate clustering of events in time or locations in space.[1]
Definition
In general, for a given sequence of events in time or space the statistic is given by:.[1]
where 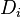 represents the interval between events or points in space and is a number between 0 and 1 such that the sum of all
represents the interval between events or points in space and is a number between 0 and 1 such that the sum of all 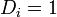 .
.
Where intervals are given by numbers that do not represent a fraction of the time period or distance, the Greenwood statistic is modified [2] and is given by:
where:
and 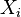 represents the length of the 'ith interval, which is either the time between events or the distances between points in space.
represents the length of the 'ith interval, which is either the time between events or the distances between points in space.
A reformulation of the statistic yields
where 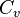 is the sample coefficient of variation of the n + 1 interval lengths.
is the sample coefficient of variation of the n + 1 interval lengths.
Properties
The Greenwood statistic is a comparative measure that has a range of values between 0 and 1. For example, applying the Greenwood statistic to the arrival of 11 buses in a given time period of say 1 hour, where in the first example all eleven buses arrived at a given point each 6 minutes apart, would give a result of roughly 0.10. However, in the second example if the buses became bunched up or clustered so that 6 buses arrived 10 minutes apart and then 5 buses arrived 2 minutes apart in the last 10 minutes, the result is roughly 0.17. The result for a random distribution of 11 bus arrival times in an hour will fall somewhere between 0.10 and 0.17. So this can be used to tell how well a bus system is running and in a similar way, the Greenwood statistic was also used to determine how and where genes are placed in the chromosomes of living organisms.[3] This research showed that there is a definite order to where genes are placed, particularly with regard to what function the genes perform, and this is important in the science of genetics.
References
- 1 2 Greenwood, Major (1946) The Statistical Study of Infectious Diseases. Journal of the Royal Statistical Society, 109(2): 85–110. JSTOR 2981176
- ↑ D'Agostino, Ralph B. and Stephens, Michael A. (1986) Goodness-of-fit techniques, Marcel Dekker, Inc., New York
- ↑ Riley, M. C. et al. (2007) Locational distribution of gene functional classes in Arabidopsis thaliana, BMC Bioinformatics. 8:112