Hahn–Kolmogorov theorem
In mathematics, the Hahn–Kolmogorov theorem characterizes when a finitely additive function with non-negative (possibly infinite) values can be extended to a bona fide measure. It is named after the Austrian mathematician Hans Hahn and the Russian/Soviet mathematician Andrey Kolmogorov.
Statement of the theorem
Let 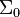 be an algebra of subsets of a set
be an algebra of subsets of a set 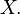 Consider a function
Consider a function
which is finitely additive, meaning that
for any positive integer N and 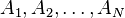 disjoint sets in
disjoint sets in 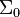 .
.
Assume that this function satisfies the stronger sigma additivity assumption
for any disjoint family 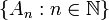 of elements of
of elements of 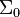 such that
such that 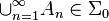 . (Functions
. (Functions 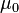 obeying these two properties are known as pre-measures.) Then,
obeying these two properties are known as pre-measures.) Then,
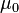 extends to a measure defined on the sigma-algebra
extends to a measure defined on the sigma-algebra 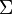 generated by
generated by 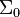 ; i.e., there exists a measure
; i.e., there exists a measure
such that its restriction to 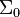 coincides with
coincides with 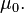
If 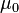 is
is 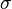 -finite, then the extension is unique.
-finite, then the extension is unique.
Non-uniqueness of the extension
If 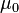 is not
is not 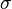 -finite then the extension need not be unique, even if the extension itself is
-finite then the extension need not be unique, even if the extension itself is 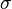 -finite.
-finite.
Here is an example:
We call rational closed-open interval, any subset of 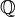 of the form
of the form 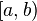 , where
, where 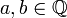 .
.
Let 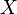 be
be 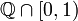 and let
and let 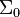 be the algebra of all finite union of rational closed-open intervals contained in
be the algebra of all finite union of rational closed-open intervals contained in 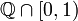 . It is easy to prove that
. It is easy to prove that 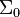 is, in fact, an algebra. It is also easy to see that every non-empty set in
is, in fact, an algebra. It is also easy to see that every non-empty set in 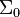 is infinite.
is infinite.
Let 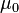 be the counting set function (
be the counting set function (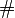 ) defined in
) defined in 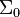 .
It is clear that
.
It is clear that 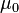 is finitely additive and
is finitely additive and 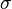 -additive in
-additive in 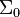 . Since every non-empty set in
. Since every non-empty set in 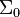 is infinite, we have, for every non-empty set
is infinite, we have, for every non-empty set 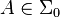 ,
, 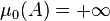
Now, let 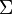 be the
be the 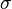 -algebra generated by
-algebra generated by 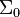 . It is easy to see that
. It is easy to see that 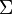 is the Borel
is the Borel 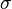 -algebra of subsets of
-algebra of subsets of 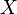 , and both
, and both 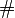 and
and 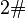 are measures defined on
are measures defined on 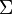 and both are extensions of
and both are extensions of 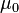 .
.
Comments
This theorem is remarkable for it allows one to construct a measure by first defining it on a small algebra of sets, where its sigma additivity could be easy to verify, and then this theorem guarantees its extension to a sigma-algebra. The proof of this theorem is not trivial, since it requires extending 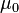 from an algebra of sets to a potentially much bigger sigma-algebra, guaranteeing that the extension is unique (if
from an algebra of sets to a potentially much bigger sigma-algebra, guaranteeing that the extension is unique (if 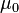 is
is 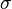 -finite), and moreover that it does not fail to satisfy the sigma-additivity of the original function.
-finite), and moreover that it does not fail to satisfy the sigma-additivity of the original function.
See also
This article incorporates material from Hahn–Kolmogorov theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
![\mu_0\colon \Sigma_0 \to[0,\infty]](../I/m/6f80635a6d7dfa6e797317a0d22e4c8a.png)
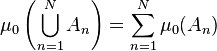
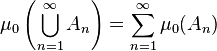
![\mu \colon \Sigma \to[0,\infty]](../I/m/a87c36f5c5affaf118790acf557cdeb7.png)