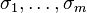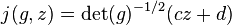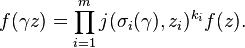Hilbert modular form
In mathematics, a Hilbert modular form is a generalization of modular forms to functions of two or more variables.
It is a (complex) analytic function on the m-fold product of upper half-planes
 satisfying a certain kind of functional equation.
satisfying a certain kind of functional equation.
Let F be a totally real number field of degree m over rational field. Let
be the real embeddings of F. Through them we have a map
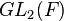 →
→ 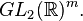
Let 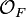 be the ring of integers of F. The group
be the ring of integers of F. The group
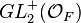 is called the full Hilbert modular group.
For every element
is called the full Hilbert modular group.
For every element 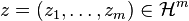 ,
there is a group action of
,
there is a group action of 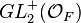 defined by
defined by
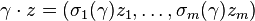
For 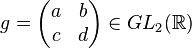 , define
, define
A Hilbert modular form of weight 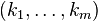 is an analytic function on
is an analytic function on
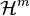 such that for every
such that for every 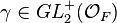
Unlike the modular form case, no extra condition is needed for the cusps because of Koecher's principle.
History
These modular forms, for real quadratic fields, were first treated in the 1901 Göttingen University Habilitationssschrift of Otto Blumenthal. There he mentions that David Hilbert had considered them initially in work from 1893-4, which remained unpublished. Blumenthal's work was published in 1903. For this reason Hilbert modular forms are now often called Hilbert-Blumenthal modular forms.
The theory remained dormant for some decades; Erich Hecke appealed to it in his early work, but major interest in Hilbert modular forms awaited the development of complex manifold theory.
References
- Paul B. Garrett: Holomorphic Hilbert Modular Forms. Wadsworth & Brooks/Cole Advanced Books & Software, Pacific Grove, CA, 1990. ISBN 0-534-10344-8
- Eberhard Freitag: Hilbert Modular Forms. Springer-Verlag. ISBN 0-387-50586-5