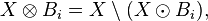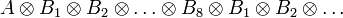Hit-or-miss transform

In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration (or pattern) in a binary image, using the morphological erosion operator and a pair of disjoint structuring elements. The result of the hit-or-miss transform is the set of positions, where the first structuring element fits in the foreground of the input image, and the second structuring element misses it completely.

Mathematical definition

In binary morphology, an image is viewed as a subset of an Euclidean space 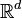$\mathbb{R}^d$ or the integer grid 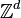$\mathbb{Z}^d$, for some dimension d. Let us denote this space or grid by E.

A structuring element is a simple, pre-defined shape, represented as a binary image, used to probe another binary image, in morphological operations such as erosion, dilation, opening, and closing.

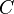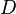Let $C$ and $D$ be two structuring elements satisfying 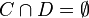$C\cap D=\emptyset$. The pair (C,D) is sometimes called a composite structuring element. The hit-or-miss transform of a given image A by B=(C,D) is given by:

$A\odot B=(A\ominus C)\cap(A^c\ominus D)$,

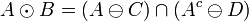where 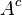$A^c$ is the set complement of A.

That is, a point x in E belongs to the hit-or-miss transform output if C translated to x fits in A, and D translated to x misses A (fits the background of A).

Some applications

Thinning

Let 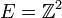$E=\mathbb{Z}^2$, and consider the eight composite structuring elements, composed of:

$C_1=\{(0,0),(-1,-1),(0,-1),(1,-1)\}$ and $D_1=\{(-1,1),(0,1),(1,1)\}$,

$C_2=\{(-1,0),(0,0),(-1,-1),(0,-1)\}$ and $D_2=\{(0,1),(1,1),(1,0)\}$

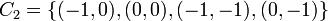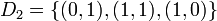
and the three rotations of each by 90°, 180°, and 270°. The corresponding composite structuring elements are denoted 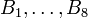$B_1,\ldots,B_8$.

For any i between 1 and 8, and any binary image X, define

$X\otimes B_i=X\setminus (X\odot B_i),$

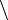where $\setminus$ denotes the set-theoretical difference.

The thinning of an image A is obtained by cyclically iterating until convergence:

$A\otimes B_1\otimes B_2\otimes\ldots\otimes B_8\otimes B_1\otimes B_2\otimes\ldots$

Other applications

• Pattern detection. By definition, the hit-or-miss transform indicates the positions where a certain pattern (characterized by the composite structuring element B) occurs in the input image.
• Pruning. The hit-or-miss transform can be used to identify the end-points of a line to allow this line to be shrunk from each end to remove unwanted branches.
• Computing the Euler number.

Bibliography

• An Introduction to Morphological Image Processing by Edward R. Dougherty, ISBN 0-8194-0845-X (1992)