Hoshen–Kopelman algorithm

Machine learning and data mining

Problems Classification Clustering Regression Anomaly detection Association rules Reinforcement learning Structured prediction Feature engineering Feature learning Online learning Semi-supervised learning Unsupervised learning Learning to rank Grammar induction
Supervised learning (classification • regression) Decision trees Ensembles (Bagging, Boosting, Random forest) k-NN Linear regression Naive Bayes Neural networks Logistic regression Perceptron Relevance vector machine (RVM) Support vector machine (SVM)
Clustering BIRCH Hierarchical k-means Expectation-maximization (EM) DBSCAN OPTICS Mean-shift
Dimensionality reduction Factor analysis CCA ICA LDA NMF PCA t-SNE
Structured prediction Graphical models (Bayes net, CRF, HMM)
Anomaly detection k-NN Local outlier factor
Neural nets Autoencoder Deep learning Multilayer perceptron RNN Restricted Boltzmann machine SOM Convolutional neural network
Reinforcement Learning Q-Learning SARSA Temporal Difference (TD)
Theory Bias-variance dilemma Computational learning theory Empirical risk minimization Occam learning PAC learning Statistical learning VC theory
Machine learning venues NIPS ICML IJMLC ML JMLR ArXiv:cs.LG
Machine learning portal

The Hoshen–Kopelman algorithm is a simple and efficient algorithm for labeling clusters on a grid. Where the grid is a regular network of cells, with the cells being either occupied or unoccupied. This algorithm is based on a well-known union-finding algorithm.^[1] The algorithm was originally described in by J. Hoshen and R. Kopelman in their 1976 paper "Percolation and Cluster Distribution. I. Cluster Multiple Labeling Technique and Critical Concentration Algorithm".^[2]

Percolation theory

Percolation theory is the study of the behavior and statistics of clusters on lattices. Suppose we have a large square lattice where each cell can be occupied with the probability p and can be empty with the probability 1 – p. Each group of neighboring occupied cells forms a cluster. Neighbors are defined as cells having a common side but not those sharing only a corner i.e. we consider 4x4 neighborhood that is top, bottom, left and right. Each occupied cell is independent of the status of its neighborhood. The number of clusters, the size of each cluster and their distribution are important topics in percolation theory.

Figure (a)

Figure (b)

Consider 5x5 grids in figure (a) and (b).
In figure (a), the probability of occupancy is p = 6/25 = 0.24.
In figure (b), the probability of occupancy is p = 16/25 = 0.64.

Hoshen–Kopelman algorithm for cluster finding

In this algorithm, we scan through a grid looking for occupied cells and labeling them with cluster labels. The scanning process is called as Raster Scan. The algorithm begins with scanning the grid cell by cell and check if the cell is occupied or not. If the cell is occupied, then it must be labeled with a cluster label. This cluster label is decided based on the neighbors of that cell. (For this we are going to use Union-Find Algorithm which is explained in the next section.) If the cell doesn’t have any occupied neighbors then, a new label is assigned to the cell.^[3]

Union-find algorithm

This algorithm is a simple method for computing equivalence classes. Calling the function union(x,y) specifies that, items x and y are members of the same equivalence class. Because equivalence relations are transitive; all the items equivalent to x are equivalent to all the items equivalent to y. Thus for any item x, there is a set of items which are all equivalent to x . This set is the equivalence class of which x is a member. A second function find(x) returns a representative member of the equivalence class to which x belongs.

Pseudo-code

During the raster scan of the grid, whenever an occupied cell is encountered, neighboring cells are scanned to check whether any of them have already been scanned. If we find already scanned neighbors, the union operation is performed, to specify that these neighboring cells are in fact members of the same equivalence class. Then thefind operation is performed to find a representative member of that equivalence class with which the current cell will be labeled.

On the other hand,if the current cell has no neighbors, it is assigned a new, previously unused, label. The entire grid is processed in this way.

Following pseudo-code is referred from Tobin Fricke's implementation of the same algorithm.^[3]

   Raster Scan and Labeling on the Grid
   largest_label = 0;
   for x in 0 to n_columns {
       for y in 0 to n_rows {
           if occupied[x,y] then
               left = occupied[x-1,y];
               above = occupied[x,y-1];
               if (left == 0) and (above == 0) then /* Neither a label above nor to the left. */
                   largest_label = largest_label + 1; /* Make a new, as-yet-unused cluster label. */
                   label[x,y] = largest_label;
               else if (left != 0) and (above == 0) then /* One neighbor, to the left. */
                   label[x,y] = find(left);
               else if (left == 0) and (above != 0) then /* One neighbor, above. */
                   label[x,y] = find(above);
               else /* Neighbors BOTH to the left and above. */
                   union(left,above); /* Link the left and above clusters. */
                   label[x,y] = find(left);
       }
   }

   Union
   void union(int x, int y)  {
       labels[find(x)] = find(y);
   }

   Find
   int find(int x)  {
       int y = x;
       while (labels[y] != y)
           y = labels[y];
       while (labels[x] != x)  {
           int z = labels[x];
           labels[x] = y;
           x = z;
       }
   return y;
   }

Example

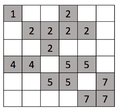
Consider the following example. The dark cells in the grid in figure (a) represent that they are occupied and the white ones are empty. So by running H–K algorithm on this input we would get the output as shown in figure (b) with all the clusters labeled.

The algorithm processes the input grid, cell by cell, as follows: Let's say that grid is a two-dimensional array.

Starting from cell grid[0][0] i.e. the first cell. The cell is occupied and it doesn't have cells to the left or above so we will label this cell with a new label say 1.
grid[0][1] and grid[0][2] both are unoccupied so they are not labeled.
grid[0][3] is occupied so check cell to the left which is unoccupied so we increment the current label value and assign the label to the cell as 2.
grid[0][4], grid[0][5] and grid[1][0] are unoccupied so they are not labeled.
grid[1][1] is occupied so check cell to the left and above, both the cells are unoccupied so assign a new label 3.
grid[1][2] is occupied so check cell to the left and above, only the cell to the left is occupied so assign the label of a cell on the left to this cell 3.
grid[1][3] is occupied so check cell to the left and above, both the cells are occupied, so merge the two clusters and assign the cluster label of the cell above to the cell on the left and to this cell i.e. 2. (Merging using union algorithm will label all the cells with label 3 to 2)
grid[1][4] is occupied so check cell to the left and above, only the cell to the left is occupied so assign the label of a cell on the left to this cell 2.
grid[1][5] , grid[2][0] and grid[2][1] are unoccupied so they are not labeled.
grid[2][2] is occupied so check cell to the left and above, only cell above is occupied so assign the label of the cell above to this cell 2.
grid[2][3] , grid[2][4] and grid[2][5] are unoccupied so they are not labeled.
grid[3][0] is occupied so check cell above which is unoccupied so we increment the current label value and assign the label to the cell as 4.
grid[3][1] is occupied so check cell to the left and above, only the cell to the left is occupied so assign the label of the cell on the left to this cell 4.
grid[3][2] is unoccupied so it is not labeled.
grid[3][3] is occupied so check cell to the left and above, both the cells are unoccupied so assign a new label 5.
grid[3][4] is occupied so check cell to the left and above, only the cell to the left is occupied so assign the label of the cell on the left to this cell 5.
grid[3][5] , grid[4][0] and grid[4][1] are unoccupied so they are not labeled.
grid[4][2] is occupied so check cell to the left and above, both the cells are unoccupied so assign a new label 6.
grid[4][3] is occupied so check cell to the left and above, both, cell to the left and above are occupied so merge the two clusters and assign the cluster label of the cell above to the cell on the left and to this cell i.e. 5. (Merging using union algorithm will label all the cells with label 6 to 5).
grid[4][4] is unoccupied so it is not labeled.
grid[4][5] is occupied so check cell to the left and above, both the cells are unoccupied so assign a new label 7.
grid[5][0]grid[5][1] grid[5][2] and grid[5][3] are unoccupied so they are not labeled.
grid[5][4] is occupied so check cell to the left and above, both the cells are unoccupied so assign a new label 8.
grid[5][5] is occupied so check cell to the left and above, both, cell to the left and above are occupied so merge the two clusters and assign the cluster label of the cell above to the cell on the left and to this cell i.e. 7. (Merging using union algorithm will label all the cells with label 8 to 7).

Figure (a)

Figure (b)

Consider 6x6 grids in figure (a) and (b).
Figure (a), This is the input to the Hoshen–Kopelman algorithm.
Figure (b), This is the output of the algorithm with all the clusters labeled.

Applications

Segmentation and Clustering of a Binary Image ^[4]
Determination of Nodal Domain Area and Nodal Line Lengths ^[5]
Nodal Connectivity Information
Modeling of electrical conduction

References

↑ https://www.cs.princeton.edu/~rs/AlgsDS07/01UnionFind.pdf
↑ Hoshen, J.; Kopelman, R. (15 October 1976). "Percolation and cluster distribution. I. Cluster multiple labeling technique and critical concentration algorithm". Phys. Rev. B. 14 (8): 3438–3445. doi:10.1103/PhysRevB.14.3438 – via APS.
1 2 "The Hoshen-Kopelman Algorithm". Ocf.berkeley.edu. 2004-04-21. Retrieved 2016-09-17.
↑ "Journal of Applied Sciences" (PDF). Scialert.net. ISSN 1812-5654. Retrieved 2016-09-17.
↑ Christian Joas. "Introduction to the Hoshen-Kopelman algorithm and its application to nodal domain statistics" (PDF). Webhome.weizmann.ac.il. Retrieved 2016-09-17.
↑ "Clustering" (PDF).
↑ "Fuzzy c-means clustering".

This article is issued from Wikipedia - version of the 10/31/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.