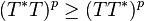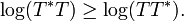Hyponormal operator
In mathematics, especially operator theory, a hyponormal operator is a generalization of a normal operator. In general, a bounded linear operator T on a complex Hilbert space H is said to be p-hyponormal (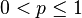 ) if:
) if:
(That is to say, 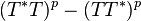 is a positive operator.) If
is a positive operator.) If 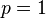 , then T is called a hyponormal operator. If
, then T is called a hyponormal operator. If 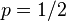 , then T is called a semi-hyponormal operator. Moreoever, T is said to be log-hyponormal if it is invertible and
, then T is called a semi-hyponormal operator. Moreoever, T is said to be log-hyponormal if it is invertible and
An invertible p-hyponormal operator is log-hyponormal. On the other hand, not every log-hyponormal is p-hyponormal.
The class of semi-hyponormal operators was introduced by Xia, and the class of p-hyponormal operators was studied by Aluthge, who used what is today called the Aluthge transformation.
Every subnormal operator (in particular, a normal operator) is hyponormal, and every hyponormal operator is a paranormal convexoid operator. Not every paranormal operator is, however, hyponormal.
See also
- Putnam’s inequality