Incremental computing

Incremental computing, also known as incremental computation, is a software feature which, whenever a piece of data changes, attempts to save time by only recomputing those outputs which depend on the changed data.^[1][2][3] When incremental computing is successful, it can be significantly faster than computing new outputs naively. For example, a spreadsheet software package might use incremental computation in its recalculation feature, to update only those cells containing formulas which depend (directly or indirectly) on the changed cells.

Incremental computing derives a new input/output pair from one or more old input/output relationships. To do so, ΔP must relate a change in the input to a change in the output. The consumer of the result may be interested in the full updated output, or the delta output, or both.

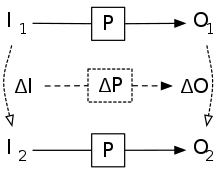
Static Versus Dynamic

Incremental computing techniques can be broadly separated into two approaches: Static approaches attempt to derive an incremental program ΔP from a conventional program P using, e.g., either automatic program transformations, or manual design. These transformations occur before any input or input changes.

Dynamic approaches record information about executing program P on a particular input (I1) and use this information when the input changes (to I2) in order to update the output (from O1 to O2). The figure shows the relationship between program P, the incremental version of this program ΔP, and a pair of inputs and outputs, I1, O1 and I2, O2.

Specialized versus General-Purpose Approaches

Some approaches to incremental computing are specialized, while others are general purpose. Specialized approaches require the programmer to explicitly specify the algorithms and data structures that will be used to preserve unchanged sub-calculations. General-purpose approaches, on the other hand, use language, compiler or algorithmic techniques to give incremental behavior to otherwise non-incremental programs.^[4]

Static Methods

Program Derivatives

Given a computation ${\displaystyle C=f(x_{1},x_{2},\dots x_{n})}$ and a potential change ${\displaystyle x_{j}:=\Delta _{x_{j}}}$, we can insert code before the change (the pre-derivative) and after the change (the post-derivative) to update the value of $C$ faster than rerunning $f$. Paige has written down a list of rules for formal differentiation of programs in SUBSETL.^[5]

View Maintenance

In database systems such as DBToaster, views are defined with relational algebra. Incremental view maintenance statically analyzes relational algebra to create update rules that quickly maintain the view in the presence of small updates, such as insertion of a row.^[6]

Dynamic Methods

A conservative (theoretically sub-optimal) implementation technique for incremental computing is for the software to build a dependency graph of all the data elements that may need to be recalculated, and their dependencies. The elements that need to be updated when a single element changes are given by the transitive closure of the dependency relation of the graph. In other words, if there is a path from the changed element to another element, the latter will be updated (even if the value does not actually change).

The dependency graph may need to be updated as dependencies change, or as elements are added to, or removed from, the system. It is used internally by the implementation, and does not typically need to be displayed to the user.

Partial evaluation can be seen as a method for automating the simplest possible case of incremental computing, in which an attempt is made to divide program data into two categories: that which can vary based on the program's input, and that which cannot (and the smallest unit of change is simply "all the data that can vary"). Of course, partial evaluation can be combined with other incremental computing techniques.

Other implementation techniques exist. For example, a topological evaluation order may be used to avoid the precomputation of elements that need to be reevaluated as in FrTime, which also avoids the problem of unnecessary updates. If a language permits cycles in the dependency graph, a single pass through the graph may not be sufficient to reach a fixed point. In many cases, complete reevaluation of a system is semantically equivalent to incremental evaluation, and may be more efficient in practice if not in theory.^[7]

Existing systems

Compiler and Language Support

• Automatic Incrementalization (also called "Self-Adjusting Computation", and "Adaptive Functional Programming"),^[8] Delta ML, Haskell Adaptive
• Cornell Synthesizer Generator^[9]
• IceDust - a custom domain-specific language.

Frameworks and libraries

• Adapton^[10] - with implementations in several languages
• One-way Dataflow Constraints (Reactive Computation in C++)
• Differential Dataflow
• Jane Street Incremental
• Incremental Datalog (Logicblox)
• Incremental Prolog (XSB)^[11]
• Domain-Specific Approaches:
  • Incremental Type Checking

Applications

• Databases (view maintenance)
• Build systems
• Spreadsheets
• Development Environments
• Financial Computations
• Attribute Grammar Evaluation
• Graph Computations and Queries
• GUIs (e.g., React and DOM diffing)
• Scientific applications

See also

• Reactive programming
• Memoization

References

1. Carlsson, Magnus (2002). "Monads for incremental computing". Proceedings of the seventh ACM SIGPLAN international conference on Functional programming. New York: ACM. pp. 26–35. doi:10.1145/581478.581482. ISBN 1-58113-487-8.
2. Umut A. Acar (2005). Self-Adjusting Computation (PDF) (Ph.D. thesis).
3. Camil Demetrescu; Irene Finocchi; Andrea Ribichini (2011). "Reactive Imperative Programming with Dataflow Constraints". Proceedings of the 26th ACM International Conference on Object-Oriented Programming Systems Languages and Applications (OOPSLA 2011). ACM. pp. 407–426. doi:10.1145/2048066.2048100. ISBN 978-1-4503-0940-0.
4. Yan Chen; Joshua Dunfield; Matthew A. Hammer; Umut A. Acar. ICFP 2011 (PDF).
5. Paige, Robert (1981). Formal Differentiation: A Program Synthesis Technique. UMI Research Press. ISBN 0-8357-1213-3.
6. Ahmad, Yanif; Kennedy, Oliver; Koch, Christoph; Nikolic, Milos (2012-06-01). "DBToaster: Higher-order Delta Processing for Dynamic, Frequently Fresh Views". Proc. VLDB Endow. 5 (10): 968–979. doi:10.14778/2336664.2336670. ISSN 2150-8097.
7. Kimberley Burchett; Gregory H. Cooper; Shriram Krishnamurthi (2007). "Lowering: A static optimization technique for transparent functional reactivity". In ACM SIGPLAN Symposium on Partial Evaluation and Semantics-Based Program Manipulation. pp. 71–80. ISBN 978-1-59593-620-2.
8. Hammer, Matthew A.; Acar, Umut A.; Chen, Yan (2009). "CEAL": 25. doi:10.1145/1542476.1542480.
9. Reps, Thomas; Teitelbaum, Tim (1984). "The synthesizer generator": 42–48. doi:10.1145/800020.808247.
10. "Adapton: Programming Language Abstractions for Incremental Computation". adapton.org. Retrieved 2016-10-07.
11. Saha, Diptikalyan; Ramakrishnan, C. R. (2005). "Incremental Evaluation of Tabled Prolog: Beyond Pure Logic Programs". 3819: 215–229. doi:10.1007/11603023_15. ISSN 0302-9743.