Input/output automaton

Input/output automata provide a formal model, applicable in describing most types of asynchronous concurrent system. On its own, the I/O automaton model contains a very basic structure that enables it to model various types of distributed systems. To describe specific types of asynchronous systems, additional structure must be added to this basic model. The model presents an explicit method for describing and reasoning about system components such as processes and message channels that interact with one another, operating at arbitrary relative speeds.^[1] The I/O automata were first introduced by Nancy A. Lynch and Mark R. Tuttle in "Hierarchical correctness proofs for distributed algorithms", 1987.^[2]

"An I/O automaton models a distributed system component that can interact with other system components. It is a simple type of state machine in which the transitions are associated with named actions."^[1] There are three types of actions: input, output, and internal actions. The automaton uses its input and output actions to communicate with its environment, whereas the internal actions are only visible to the automaton itself. Unlike internal and output actions that are selected and carried out by the automaton, the input actions – which simply arrive from the environment - are not under automaton's control.^[1]

Examples

I/O automata can be used to model individual components of a distributed system, such as a process, a message channel in a message passing system, or a shared data structure in a shared memory systems.

Process I/O automaton

Figure 1: Process I/O Automaton

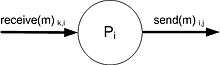
Figure 1 depicts an example of an I/O automaton for a process in an asynchronous message-passing distributed system. In this setting, process P_i communicates with other processes by using a message passing system. Its output actions are of the form send(m)_i,j, which represents process P_i sending a message with contents m to process P_j. The input actions are of form receive(m)_k,i, representing the receipt of message with contents m by process P_i from process P_k. (The internal actions of P_i, which would correspond to the algorithm that the process is running are not shown.)

FIFO message channel

Figure 2: FIFO Channel I/O Automaton

A message channel can also be modelled by an I/O automaton. Figure 2 illustrates a typical unidirectional FIFO channel automaton, named C_i,j. It has input actions of the form send(m)_i,j, and output actions of the form receive(m)_i,j. Each message m may contain 0 or 1 (m ∈ {0,1}). The state of the automaton stores a FIFO queue of all messages that have been sent but not yet received.

In a typical distributed system where both process automata and communication channel automata exist, they are composed in a way that output actions of one automaton are matched and executed with identically-named input actions of the other automata. For example, consider a system composed of two process, P_i and P_j, and a communication channel C_i,j from process P_i to process P_j. In this setting, process P_i executes the output action send(m)_i,j, if and only if channel C_i,j also executes its send(m)_i,j input action.

Atomic read/write register

Figure 3: Atomic Read/Write Register I/O Automaton

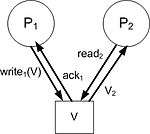
Figure 3 illustrates an atomic read/write register I/O automaton in a shared memory system with two processes, P₁ and P₂. The value V stored in the register is of type integer (V ∈ Z). The state of the automaton stores this value. Input actions consist of write_i(V), which represents process P_i requesting to write a value V to the register (where i ∈ {1,2} and V ∈ Z), and read_i, which corresponds to a process P_i requesting to read the value currently stored in the register. The output action ack_i is used to inform process P_i that the write request has successfully completed. The output action V_i represents the value V being returned as a response to a read request by process P_i.

The automaton also includes internal actions perform_Write(V), which writes the value V to the register (by updating the state of the automaton), and perform_Read, which is used to read the value V stored in the state. (These internal actions are not shown in Figure 3.)

Formal specification

An I/O automaton A, or simply an automaton, comprises five components:

• sig(A)
• states(A)
• start(A)
• trans(A)
• tasks(A)^[1][3]

These five components are described below.

Signature

The initial step in formalization of an I/O automaton A is the definition of its signature, sig(A). A signature S describes the I/O automaton's actions using three disjoint sets of actions:

1. in(S): input actions,
2. out(S): output actions, and
3. int(S): internal actions.

Based on the above formalization of input, output and internal actions, it is possible to define the following objects.

• ext(S): the external actions, defined as in(S) ∪ out(S)
• local(S): the locally controlled actions, defined as out(S) ∪ int(S)
• extsig(S): the external signature, defined as (in(S), out(S), ø)
• acts(S) is defined as the set of all the actions of signature S.^[1][3]

States

The set of states of automaton A, denoted states(A), need not be finite. This is a significant generalization of the usual notion of finite automata, as it enables modeling systems with unbounded data structures like counters and unbounded length queues. The set of start states (also known as initial states) is a non-empty subset of states. Multiple start states are allowed so that some input information can be included in the start states.^[1][3]

Transition relation

The state-transition relation of automaton A is denoted trans(A) ⊆ states(A) × acts(sig(A)) × states(A). It satisfies the property that "for every state s and every input action π, there is a transition (s, π, s') ∈ trans(A)."

A transition, also known as a step of I/O automaton A, is defined as an element (s, π, s') of trans(A). An input transition refers to a transition (s, π, s') when π is an input action, output transition indicates a transition (s, π, s') when π is an output action and so on. For any state s and action π, if the I/O automaton A has some transition of the form (s, π, s'), then π is said to be enabled in s. I/O automata are described as input-enabled because all input actions are required to be enabled in every state. A quiescent state s is defined as a state where only input actions are enabled.^[1][3]

Tasks

The fifth component of the I/O automaton A, tasks (A), is a task partition, defined as an equivalence relation on locally controlled actions of A, which has at most countably many equivalence classes. Informally, the task partition tasks(A), represents an abstract description of "tasks," or "threads of control," within A.

This partition is used to define fairness conditions on an execution of the automaton. These conditions require the automaton to continue giving fair turns to each of its tasks during its execution. This is particularly helpful when modelling a system component that performs multiple jobs. For instance, a component that participates in an ongoing algorithm while periodically reporting status information to its environment simultaneously would have two tasks. The partition is also useful when several automata are composed (to produce a larger system automaton) when specifying that the all automata in the composition continue to take steps in the composed system.^[1][3]

Example: Formal definition of channel I/O automaton

As described above, C_i,j is an example of I/O automaton that represents a unidirectional FIFO channel from process P_i to process P_j. Let m be a binary message: m ∈ {0,1}. The automaton C_i,j can be formally defined as follows.

Signature:

sig(C_i,j) specifies that the automaton has two kinds of actions:

• An input action of (C_i,j) is of the form send(m)_i,j, where m ∈ {0,1}.
• An output action of (C_i,j) is of the form receive(m)_i,j, where m ∈{0,1}.

Intuitively, the action send(m)_i,j indicates that a message m has entered the channel when it is sent by process P_i and the action receive(m)_i,j indicates that a message m has left the channel when it is delivered to process P_j.^[1]

States:

states(C_i,j) is the set of all finite sequences of elements m ∈ {0,1}. Intuitively, the state represents the sequence of messages currently en route from the sender, process P_i, to the receiver, process P_j, in the order they were sent.

start(C_i,j), representing the initial states of the queue, contains only the empty sequence.^[1]

Transitions

The transition relation can be modelled in a precondition-effect style, where all the transitions that include each specific type of action are grouped into a single piece of code. In this code, the conditions which must be satisfied before allowing an action to occur, are formalized as a predicate on the pre-state s, which is the state before the action occurs. Consequent changes to the state that result from the execution of the action are coded in the form of a simple program. This program is executed indivisibly, as a single transition. If this program is applied to the state s, the new state s' results.

The transitions of C_i,j are described as:

for send(m)_i,j:

• Precondition: None
• Effect: m is added to the end of the sequence stored in the state (where m ∈ {1,0})

for receive(m)_i,j:

• Precondition: m is the first element in the sequence stored in the state (where m ∈ {1,0})
• Effect: remove the first element of the sequence stored in the state

Intuitively, the send action can be executed any time; it causes the addition of the message m to the end of the queue of messages in che channel. The receive action removes and returns the first element of the queue.^[1]

Tasks

tasks(C_i,j), represents a task partition that groups together all actions of form receive into a single task. Intuitively, handing over messages to process P_j is considered as a single task.

{receive(m)i,j : m ∈ {0,1}}.^[1]

Execution and trace

Execution

In a run of an automaton, a string is generated that describes the behaviour of the component the automaton models.^[3] "An execution fragment of I/O Automaton A is either

• a finite sequence, s₀, π₁, s₁, π₂,... , π_r, s_r, or
• an infinite sequence, s₀, π₁, s₁,π₂,...,π_r,s_r,...,

of alternating states and actions of A such that (s_k, π_k+1, s_k+1) is a transition of A for every k ≥ 0."

A finite sequence must terminate with a state. An execution is defined as an execution fragment that begins with start state. The set of executions of A is represented by execs(A). A reachable state in I/O automaton A is the final state of a finite execution of A.

Assume α is a finite execution fragment of A ending with state s_f. Assume further that α' is any execution fragment of A that begins with s_f, the last state of α. In this case, the sequence produced by concatenating α and α', and eliminating the duplicate occurrence of s_f, the last state of α, is represented by α.α' . This sequence is also an execution fragment of I/O automaton A.^[1]

Trace

A trace of an I/O automaton A is the sequence of external actions that occurs in some execution α of A. The set of all traces of A is represented as traces(A).^[1]

Example: Three executions

Executions a, b and c are three executions of the automaton C_i,j described in Formal Definition of Channel I/O Automaton (where message m ∈ {0, 1}). In this example, the states are indicated by putting the sequence of messages in queue in brackets; the empty sequence is represented by λ.

(a) [λ], send(1)_i,j, [1], receive(1)_i,j, [λ], send(0)_i,j, [0], receive(0)_i,j, [λ]

(b) [λ], send(1)_i,j, [1], receive(1)_i,j, [λ], send(0)_i,j, [0]

(c) [λ], send(1)_i,j, [1], send(1)_i,j, [11], send(0)_i,j, [110]....^[1]

Operations on automata

Composition operation

It is possible to compose several automata, each describing individual system components, to yield an automaton that represents a larger, more complex system. In this case, actions that have the same name in each constituent automata are identified together. Therefore, when a component automata takes a step that includes an action π, all other component automata with π in their signatures also perform that action. The following outlines the conditions for composition of automata A and A' to be permitted:

1. The internal actions of A must be disjoint from actions of A’. This prevents performance of a step in A’ when the internal actions of A – with the same name as actions of A' - are performed.
2. The output actions of A and A’ must be disjoint. This condition ensures that only one constituent automaton controls performance of an output action.

If the composition is constructed from a countably infinite collection of automata, then there is an additional constraint: each action needs to be an action of only finitely many of the constituent automata. Infinite composition of automata allows modeling of logical systems that may be constructed from many logical components. The logical system is often implemented on a physical system that contains fewer components.^[1]

Example: Composition

Figure 4: Composition

Figure 4 depicts a composition of two processes, P_i and P_j and a FIFO message channel C_i,j, matching output actions of one automaton with identically named input actions of other automata. Thus, a send(m)_i,j output performed by process P_i is matched and performed with a send(m)_i,j input performed by channel C_i,j.

Process P_i sends the message m, where m ∈{1,0} via channel C_i,j to Process P_j. Process P_j reverses the bit in the received message m from P_i using its internal action reverse - not shown in the picture - and forwards the message to other parts of the system.

Hiding operation

It is possible to hide the output actions of an I/O automaton through "reclassifying them as internal actions." This has the effect of excluding them from communication with other parts of the system. Formally, the hiding operation for signatures is described as follows:

Let S be a signature and Φ ⊆ out(S). hide_Φ(S) is the new signature S', where

• in(S')= in(S)
• out(S')= out(S) - Φ
• int(S') =int(S) ∪ Φ

Therefore, "If A is an automaton and Φ ⊆ out(A), then hide_Φ(A) is the automaton A' obtained from A by replacing sig(A) with sig(A') = hide_Φ(sig(A))."^[1]

Fairness

Recall that a task partition is defined as an equivalence relation on an I/O automaton’s locally controlled actions, containing at most countably many equivalence classes. In this setting, fairness can be defined as continuously providing each task with a chance to perform an action.

In an I/O automaton A, let C represent a class of tasks(A). Formally, an execution fragment α of A is considered fair if the below criteria hold for every class C:

1. "If α is finite, then C is not enabled in the final state of α."
2. "If α is infinite, then α contains either infinitely many events from C or infinitely many occurrences of states in which C is not enabled."

An event is defined as the "occurrence of an action in a sequence, for example, an execution or a trace." Based on the definition of fairness, "infinitely often," each task (or equivalence class C) gets a chance to perform an action. When a task (or equivalence class) C does get a chance to perform an action, two cases are possible: an action in C is enabled in current state and can be performed, or none of the actions in C are enabled in the current state and therefore, can not be performed. Thus, a finite fair execution with final state S_f can be defined as an execution where the automaton continuously gives turns to all tasks in a round-robin fashion, but no actions are executed as none are enabled in S_f.

The set of fair executions of I/O automaton A is represented by fairexecs(A). Let β be the trace of a fair execution of A. Then β is a fair trace of A. The set fair traces of A is represented by fairtraces(A).

In the execution example, execution (a) is fair, since in its final state no receive action is enabled. Execution (b) is finite, yet a receive action is enabled in its final state. Therefore, execution (b) is not fair. Execution (c) is infinite, does not contain receive events, and at all points after the first step, receive actions are enabled. Therefore, it is not a fair execution.^[1][3] The definition of fairness has a significant property: "the fair executions of a composition are the composition of the fair executions of the components:" that is, Fair(∏_i A_i)= ∏_i Fair(A_i).^[2]

Properties and proof methods

I/O automata provide an accurate description of asynchronous systems. They are also used to formalize and prove "precise claims" about "what systems can do." In this section, a number of important types of properties are described. These, as well as further properties and proof methods, are explained in Distributed Algorithms.^[1]

Input enabling properties

The input enabling property states that the automaton cannot block input actions from happening. The two significant advantages of having this property are:

1. As the model is designed to cope with arbitrary inputs, a major source of system errors due to a failure in handling unexpected inputs is eliminated.
2. The input-enabling property makes use of "simple notions of external behavior for an automaton, based on sequences of external actions." Proofs of certain theorems in the model might fail without the assumption of this property.

Trace properties

As internal actions of an I/O automaton are invisible to a user; the I/O automaton appears to be a black box and the user merely sees "traces of automaton's executions (or fair executions)." Certain properties of I/O automata and their proofs are typically formalized as "properties of their traces or fair traces."

Let P be a trace property; P has the following components:

• sig(P), that represents a signature with no internal actions
• traces(P), that corresponds to a set of "sequences of actions in acts(sig(P))." This set may be infinite.

The trace property describes an external signature as well as a set (or a property) of sequences viewed at that interface. Sometimes acts(sig(P)) is represented by a shorthand notation acts(P). When it is mentioned that I/O automaton A satisfies a trace property P, (at least) two different meanings might be intended:

1. "extsig(A) = sig(P) and traces(A) ⊆ traces(P)"
2. "extsig(A) = sig(P) and fairtraces(A) ⊆ traces(P)"

Intuitively, it means that when A generates an external behavior then that is allowed by Property P. However, it is not required for A to actually represent every trace of P. Since A is input-enabled, then for every possible sequence of input actions, the fairtraces(A) (and so traces(A)) includes a response by A. If fairtraces(A) ⊆ traces(P) holds, then property P must contain all of the generated sequences.

Safety properties

Intuitively, a safety property represents the fact that nothing "bad" happens. More formally, Let P be a trace property. P is a trace safety property, or safety property, if the following criteria hold for traces(P).

• traces(P) is not empty: Something bad cannot happen prior to occurrence of any events; therefore, having non-emptiness is a reasonable condition on traces(P).
• traces(P) is "prefix-closed": Let β ∈ traces(P) and β' represent a finite prefix of β In this case, β' ∈ traces(P). To elaborate, assume there is a trace in which nothing bad happens. Therefore, nothing bad happens in any prefix of that trace. Thus, having prefix-closure is a reasonable condition on traces(P).
• traces(P) is "limit-closed": Let β₁, β₂, . . . represent an infinite sequence of finite sequences in traces(P). Also, assume that for each i, β_i is a prefix of β_i+1. In this case, the unique sequence β, that is "the limit of the β_i under the successive extension ordering" also exists in traces (P). Therefore, if something bad were to happen in a trace, then it would be the result of certain specific event in the trace. Having limit closure in this case is thus a reasonable condition on traces(P).

Liveness properties

Informally, a liveness property can be interpreted as something "good" eventually happens. Therefore, regardless of what has happened to a certain point in time, something good can happen at some time in the future. More formally, let P be a trace property. P is a trace liveness property, or a liveness property, "if every finite sequence over acts(P) has some extension in traces(P)."

Further reading

• Timed I/O Automaton: Merritt, Michael; Modugno, Francesmary; Tuttle, Mark R. (August 1991). "Time constrained automata (Extended Abstract)". Proceedings of the 2nd International Conference on Concurrency Theory. CONCUR '91. 527. pp. 408–423.
• Probabilistic I/O Automaton: Wu, Sue-Hwey; Smolka, Scott A.; Stark, Eugene W. (April 1997). "Composition and behaviors of probabilistic I/O automata" (PDF). Theoretical Computer Science. 176 (1-2): 1–38. doi:10.1016/s0304-3975(97)00056-x.

See also

• Communicating sequential processes
• Actor model

References

1. Lynch, Nancy (1996). Distributed Algorithms (1st ed.). San Francisco, CA: Morgan Kaufmann Publishers. ISBN 978-1-55860-348-6.
2. Lynch, Nancy A.; Tuttle, Mark R. (August 1987). "Hierarchical correctness proofs for distributed algorithms". Proceedings of the sixth annual ACM Symposium on Principles of distributed computing. PODC '87. pp. 137–151.
3. Lynch, Nancy A.; Tuttle, Mark R. (September 1989). "An introduction to input/output automata" (PDF). CWI-Quarterly. 2 (3): 219–246.