Jamshidian's trick

Jamshidian's trick is a technique for one-factor asset price models, which re-expresses an option on a portfolio of assets as a portfolio of options. It was developed by Farshid Jamshidian in 1989.

The trick relies on the following simple, but very useful mathematical observation. Consider a sequence of monotone (increasing) functions 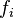$f_i$ of one real variable (which map onto 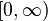$[0,\infty)$), a random variable 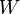$W$, and a constant $K\ge0$.

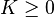Since the function 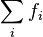$\sum_i f_i$ is also increasing and maps onto 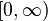$[0,\infty)$, there is a unique solution 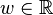$w\in\mathbb{R}$ to the equation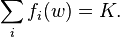 $\sum_i f_i(w)=K.$

Since the functions 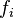$f_i$ are increasing: $\left(\sum_i f_i(W)-K\right)_+ = \left(\sum_i (f_i(W)-f_i(w))\right)_+ = \sum_i (f_i(W)-f_i(w))1_{\{W\ge w\}} = \sum_i(f_i(W)-f_i(w))_+.$

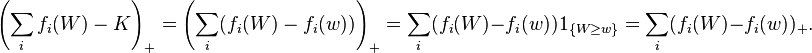
In financial applications, each of the random variables 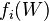$f_i(W)$ represents an asset value, the number 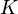$K$ is the strike of the option on the portfolio of assets. We can therefore express the payoff of an option on a portfolio of assets in terms of a portfolio of options on the individual assets 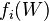$f_i(W)$ with corresponding strikes $f_i(w)$.

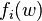References

• Jamshidian, F. (1989). "An exact bond option pricing formula," Journal of Finance, Vol 44, pp 205-209