Jessen's icosahedron
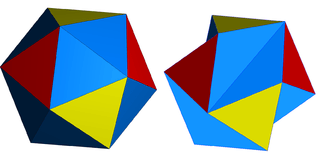
The regular icosahedron and the Jessen's icosahedron.
Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, is a non-convex polyhedron with the same number of vertices, edges and faces as the regular icosahedron. It was introduced by Børge Jessen in 1967 and has several interesting geometric properties:
- It is vertex-transitive (or isogonal), meaning that it has symmetries taking any vertex to any other vertex.
- It has only right dihedral angles.
- It is (continuously) rigid but not infinitesimally rigid. That is, in less formal language, it is a shaky polyhedron.
- As with the simpler Schönhardt polyhedron, its interior cannot be triangulated into tetrahedra without adding new vertices.
- It is scissors-congruent to a cube, meaning that it can be sliced into smaller polyhedral pieces that can be rearranged to form a solid cube.
Although a shape resembling Jessen's icosahedron can be formed by keeping the vertices of a regular icosahedron in their original positions and replacing certain pairs of equilateral-triangle faces by pairs of isosceles triangles, the resulting polyhedron does not have right-angled dihedrals. The vertices of Jessen's icosahedron are perturbed from these positions in order to give all the dihedrals right angles.
See also
References
- B. Jessen, Orthogonal Icosahedra, Nordisk Mat. Tidskr. 15 (1967), pp. 90–96.
- Peter R. Cromwell, Polyhedra, Cambridge University Press, (1997) pp. ?
- M. Goldberg, Unstable Polyhedral Structures, Math. Mag. 51 (1978), pp. 165–170
- Wells, D. The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin, (1991). p. 161.
External links
This article is issued from Wikipedia - version of the 6/4/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.