k-cell (mathematics)
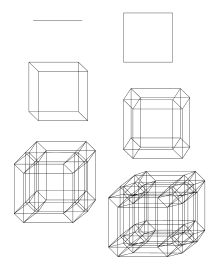
A k-cell is a higher-dimensional version of a rectangle or rectangular solid. It is the Cartesian product of k closed intervals on the real line.[1] This essentially means that is a k-dimensional rectangular solid, with each of its edges being equal to one of the closed intervals used in the definition. The k intervals need not be identical. For example, a 2-cell is a rectangle in R2 such that the sides of the rectangles are parallel to the coordinate axes.
Formal definition
Let ai ∈ R and bi ∈ R. If ai < bi for all i = 1,...,k, the set of all points x = (x1,...,xk) in Rk whose coordinates satisfy the inequalities ai ≤ xi ≤ bi is a k-cell.[2] Every k-cell is compact.[3]
Intuition
A k-cell of dimension k ≤ 3 is especially simple. For example, a 1-cell is simply the interval [a,b] with a < b. A 2-cell is the rectangle formed by the Cartesian product of two closed intervals, and a 3-cell is a rectangular solid.
Note that the sides and edges of a k-cell need not be equal in (Euclidean) length; although the unit cube (which has boundaries of equal Euclidean length) is a 3-cell, the set of all 3-cells with equal-length edges is a strict subset of the set of all 3-cells.
References
- ↑ Foran, James (1991-01-07). Fundamentals of Real Analysis. CRC Press. pp. 24–. ISBN 9780824784539. Retrieved 23 May 2014.
- ↑ Rudin, W: Principles of Mathematical Analysis, page 31. McGraw-Hill, 1976.
- ↑ Rudin, W: Principles of Mathematical Analysis, page 39. McGraw-Hill, 1976.