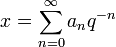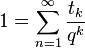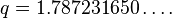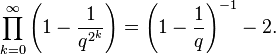Komornik–Loreti constant

The Komornik–Loreti constant is a mathematical constant that represents the smallest number for which there still exists a unique q-development.

Definition

Given a real number q > 1, the series

$x = \sum_{n=0}^\infty a_n q^{-n}$

is called the q-expansion, or 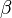$\beta$-expansion, of the positive real number x if, for all 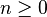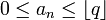$n \ge 0$, $0 \le a_n \le \lfloor q \rfloor$, where 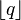$\lfloor q \rfloor$ is the floor function and 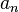$a_n$ need not be an integer. Any real number 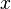$x$ such that 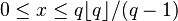$0 \le x \le q \lfloor q \rfloor /(q-1)$ has such an expansion, as can be found using the greedy algorithm.

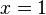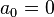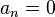The special case of $x = 1$, $a_0 = 0$, and $a_n = 0$ or 1 is sometimes called a 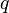$q$-development. 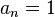$a_n = 1$ gives the only 2-development. However, for almost all 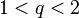$1 < q < 2$, there are an infinite number of different 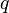$q$-developments. Even more surprisingly though, there exist exceptional 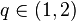$q \in (1,2)$ for which there exists only a single 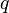$q$-development. Furthermore, there is a smallest number 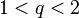$1 < q < 2$ known as the Komornik–Loreti constant for which there exists a unique 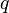$q$-development.^[1]

The Komornik–Loreti constant is the value 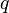$q$ such that

$1 = \sum_{n=1}^\infty \frac{t_k}{q^k}$

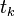where $t_k$ is the Thue–Morse sequence, i.e., 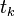$t_k$ is the parity of the number of 1's in the binary representation of 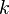$k$. It has approximate value

$q=1.787231650\ldots. \,$

The constant 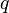$q$ is also the unique positive real root of

$\prod_{k=0}^\infty \left ( 1 - \frac{1}{q^{2^k}} \right ) = \left ( 1 - \frac{1}{q} \right )^{-1} - 2.$

This constant is transcendental.^[2]

References

1. Weissman, Eric W. "q-expansion" From Wolfram MathWorld. Retrieved on 2009-10-18.
2. Weissman, Eric W. "Komornik–Loreti Constant." From Wolfram MathWorld. Retrieved on 2010-12-27.