Langley’s Adventitious Angles

Langley’s Adventitious Angles

Langley’s Adventitious Angles is a mathematical problem posed by Edward Mann Langley in the Mathematical Gazette in 1922.[1][2]

The problem

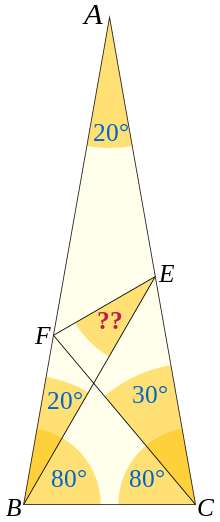
In its original form the problem was as follows: ABC is an isosceles triangle. B = C = 80 degrees. CF at 30 degrees to AC cuts AB in F. BE at 20 degrees to AB cuts AC in E. Prove angle BEF = 30 degrees.[2][3]

Solution

A solution was developed by James Mercer in 1923: Draw BG at 20 degrees to BC cutting CA in G. Then angle GBF = 60 degrees and angles BGC and BCG are 80 degrees. So BC = BG. Also angle BCF = angle BFC = 50 degrees, so BF = BG and triangle BFG is equilateral. But angle GBE = 40 degrees = angle BEG, so BG = GE = GF. And angle FGE = 40 degrees, hence GEF = 70 degrees and BEF = 30 degrees.[2]

Generalization

A quadrilateral such as BCEF in which the angles formed by all pairs of the six lines joining any two vertices, are rational multiples of π radians, i.e. n*180°/m, is called an adventitious quadrangle. Several constructions for other adventitious quadrangles, beyond the one appearing in Langley's puzzle, are known. They form several infinite families and an additional set of sporadic examples.[4]

Classifying the adventitious quadrangles (which need not be convex) turns out to be equivalent to classifying all triple intersections of diagonals in regular polygons. This was solved by Gerrit Bol in 1936 (Beantwoording van prijsvraag # 17, Nieuw-Archief voor Wiskunde 18, pages 14-66). He in fact classified (though with a few errors) all multiple intersections of diagonals in regular polygons. His results (all done by hand!) were confirmed with computer, and the errors corrected, by Bjorn Poonen and Michael Rubinstein in 1998.[5] The article contains a history of the problem and a remarkable picture featuring the regular 30-gon. "aerile re" which is active on yahoo"知恵袋" solved the unsolved adventitious quadrangles by the method of 3 circumcenters.[6][7]

References

  1. ↑ Langley, E. M. (1922), "Problem 644", The Mathematical Gazette, 11: 173.
  2. 1 2 3 Darling, David (2004), The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes, John Wiley & Sons, p. 180.
  3. ↑ Tripp, Colin (1975), "Adventitious angles", The Mathematical Gazette, 59: 98–106, JSTOR 3616644.
  4. ↑ Rigby, J. F. (1978), "Adventitious quadrangles: a geometrical approach", The Mathematical Gazette, 62 (421): 183–191, doi:10.2307/3616687, MR 513855.
  5. ↑ "The number of intersection points made by the diagonals of a regular polygon", SIAM Journal on Discrete Mathematics 11, #1, pages 135-156
  6. ↑ Hiroshi, Saito (2016), "The adventitious quadrangles was solved completely by the elementary solution", 現代数学: 66–73
  7. ↑ http://note.chiebukuro.yahoo.co.jp/detail/n365238?fr=pc_tw_share_n

External links

This article is issued from Wikipedia - version of the 10/24/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.