Lauricella's theorem
In the theory of orthogonal functions, Lauricella's theorem provides a condition for checking the closure of a set of orthogonal functions, namely:
Theorem. A necessary and sufficient condition that a normal orthogonal set 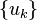 be closed is that the formal series for each function of a known closed normal orthogonal set
be closed is that the formal series for each function of a known closed normal orthogonal set 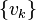 in terms of
in terms of 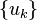 converge in the mean to that function.
converge in the mean to that function.
The theorem was proved by Giuseppe Lauricella in 1912.
References
- G. Lauricella: Sulla chiusura dei sistemi di funzioni ortogonali, Rendiconti dei Lincei, Series 5, Vol. 21 (1912), pp. 675–85.
This article is issued from Wikipedia - version of the 12/9/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.