Lax functor

In category theory, a discipline within mathematics, the notion of lax functor between bicategories generalizes that of functors between categories.

Let C,D be bicategories. We denote composition in diagrammatic order. A lax functor P from C to D, denoted 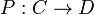$P: C\to D$, consists of the following data:

• for each object x in C, an object $P_x\in D$;
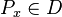• for each pair of objects x,y ∈ C a functor on morphism-categories, $P_{x,y}: C(x,y)\to D(P_x,P_y)$;
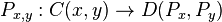• for each object x∈C, a 2-morphism 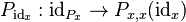$P_{\text{id}_x}:\text{id}_{P_x}\to P_{x,x}(\text{id}_x)$ in D;
• for each triple of objects, x,y,z ∈C, a 2-morphism 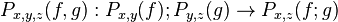$P_{x,y,z}(f,g): P_{x,y}(f);P_{y,z}(g)\to P_{x,z}(f;g)$ in D that is natural in f: x→y and g: y→z.

These must satisfy three commutative diagrams, which record the interaction between left unity, right unity, and associativity between C and D. See http://ncatlab.org/nlab/show/pseudofunctor.

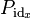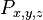A lax functor in which all of the structure 2-morphisms, i.e. the $P_{\text{id}_x}$ and $P_{x,y,z}$ above, are invertible is called a pseudofunctor.