Lee Hwa Chung theorem
The Lee Hwa Chung theorem is a theorem in symplectic topology.
The statement is as follows. Let M be a symplectic manifold with symplectic form ω. Let 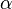 be a differential k-form on M which is invariant for all Hamiltonian vector fields. Then:
be a differential k-form on M which is invariant for all Hamiltonian vector fields. Then:
- If k is odd,
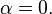
- If k is odd,
- If k is even,
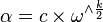 , where
, where 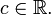
- If k is even,
References
- Lee, John M., Introduction to Smooth Manifolds, Springer-Verlag, New York (2003) ISBN 0-387-95495-3. Graduate-level textbook on smooth manifolds.
This article is issued from Wikipedia - version of the 4/17/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.