McKay graph

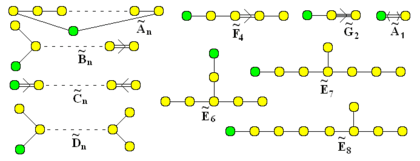Affine (extended) Dynkin diagrams

In mathematics, the McKay graph of a finite-dimensional representation V of a finite group G is a weighted quiver encoding the structure of the representation theory of G. Each node represents an irreducible representation of G. If ${\displaystyle \chi _{i},\chi _{j}}$ are irreducible representations of G then there is an arrow from $\chi _{i}$ to ${\displaystyle \chi _{j}}$ if and only if ${\displaystyle \chi _{j}}$ is a constituent of the tensor product ${\displaystyle V\otimes \chi _{i}}$. Then the weight n_ij of the arrow is the number of times this constituent appears in ${\displaystyle V\otimes \chi _{i}}$. For finite subgroups H of GL(2, C), the McKay graph of H is the McKay graph of the canonical representation of H.

If G has n irreducible characters, then the Cartan matrix c_V of the representation V of dimension d is defined by ${\displaystyle c_{V}=(d\delta _{ij}-n_{ij})_{ij}}$, where δ is the Kronecker delta. A result by Steinberg states that if g is a representative of a conjugacy class of G, then the vectors ${\displaystyle ((\chi _{i}(g))_{i}}$ are the eigenvectors of c_V to the eigenvalues ${\displaystyle d-\chi _{V}(g)}$, where ${\displaystyle \chi _{V}}$ is the character of the representation V.

The McKay correspondence, named after John McKay, states that there is a one-to-one correspondence between the McKay graphs of the finite subgroups of SL(2, C) and the extended Dynkin diagrams, which appear in the ADE classification of the simple Lie Algebras.

Definition

Let G be a finite group, V be a representation of G and $\chi$ be its character. Let ${\displaystyle \{\chi _{1},\ldots ,\chi _{d}\}}$ be the irreducible representations of G. If

${\displaystyle V\otimes \chi _{i}=\sum _{j}n_{ij}\chi _{j},}$

then define the McKay graph ${\displaystyle \Gamma _{G}}$ of G as follow:

• To each irreducible representation of G corresponds a node in ${\displaystyle \Gamma _{G}}$.
• There is an arrow from $\chi _{i}$ to ${\displaystyle \chi _{j}}$ if and only if n_ij > 0 and n_ij is the weight of the arrow: ${\displaystyle \chi _{i}{\xrightarrow {n_{ij}}}\chi _{j}}$.
• If n_ij = n_ji, then we put an edge between ${\displaystyle \chi _{i}}$ and ${\displaystyle \chi _{j}}$ instead of a double arrow. Moreover, if n_ij = 1, then we do not write the weight of the corresponding arrow.

We can calculate the value of n_ij by considering the inner product. We have the following formula:

${\displaystyle n_{ij}=\langle V\otimes \chi _{i},\chi _{j}\rangle ={\frac {1}{|G|}}\sum _{g\in G}V(g)\chi _{i}(g){\overline {\chi _{j}(g)}},}$

where $\langle \cdot ,\cdot \rangle$ denotes the inner product of the characters.

The McKay graph of a finite subgroup of GL(2, C) is defined to be the McKay graph of its canonical representation.

For finite subgroups of SL(2, C), the canonical representation is self-dual, so n_ij = n_ji for all i, j. Thus, the McKay graph of finite subgroups of SL(2, C) is undirected.

In fact, by the McKay correspondence, there is a one-to-one correspondence between the finite subgroups of SL(2, C) and the extended Coxeter-Dynkin diagrams of type A-D-E.

We define the Cartan matrix c_V of V as follow:

${\displaystyle c_{V}=(d\delta _{ij}-n_{ij})_{ij},}$

where $\delta _{ij}$ is the Kronecker delta.

Some results

• If the representation V of a finite group G is faithful, then the McKay graph of V is connected.
• The McKay graph of a finite subgroup of SL(2, C) has no self-loops, that is, n_ii = 0 for all i.
• The weights of the arrows of the McKay graph of a finite subgroup of SL(2, C) are always less or equal than one.

Examples

• Suppose G = A × B, and there are canonical irreducible representations c_A and c_B of A and B respectively. If $\chi _{i}$, i = 1, ..., k, are the irreducible representations of A and $\psi _{j}$, j = 1, ..., l, are the irreducible representations of B, then

${\displaystyle \chi _{i}\times \psi _{j}\quad 1\leq i\leq k,\,\,1\leq j\leq l}$

are the irreducible representations of $A\times B$, where ${\displaystyle \chi _{i}\times \psi _{j}(a,b)=\chi _{i}(a)\psi _{j}(b),(a,b)\in A\times B}$. In this case, we have

${\displaystyle \langle (c_{A}\times c_{B})\otimes (\chi _{i}\times \psi _{l}),\chi _{n}\times \psi _{p}\rangle =\langle c_{A}\otimes \chi _{k},\chi _{n}\rangle \cdot \langle c_{B}\otimes \psi _{l},\psi _{p}\rangle .}$

Therefore, there is an arrow in the McKay graph of G between ${\displaystyle \chi _{i}\times \psi _{j}}$ and ${\displaystyle \chi _{k}\times \psi _{l}}$ if and only if there is an arrow in the McKay graph of A between $\chi _{i}$ and $\chi_k$ and there is an arrow in the McKay graph of B between $\psi _{j}$ and $\psi _{l}$. In this case, the weight on the arrow in the McKay graph of G is the product of the weights of the two corresponding arrows in the McKay graphs of A and B.

• Felix Klein proved that the finite subgroups of SL(2, C) are the binary polyhedral groups. The McKay correspondence states that there is a one-to-one correspondence between the McKay graphs of these binary polyhedral groups and the extended Dynkin diagrams. For example, let $\overline {T}$ be the binary tetrahedral group. Every finite subgroup of SL(2, C) is conjugate to a finite subgroup of SU(2, C). Consider the matrices in SU(2, C):

${\displaystyle S=\left({\begin{array}{cc}i&0\\0&-i\end{array}}\right),V=\left({\begin{array}{cc}0&i\\i&0\end{array}}\right),U={\frac {1}{\sqrt {2}}}\left({\begin{array}{cc}\epsilon &\epsilon ^{3}\\\epsilon &\epsilon ^{7}\end{array}}\right),}$

where ε is a primitive eighth root of unity. Then, $\overline {T}$ is generated by S, U, V. In fact, we have

${\displaystyle {\overline {T}}=\{U^{k},SU^{k},VU^{k},SVU^{k}|k=0,\ldots ,5\}.}$

The conjugacy classes of $\overline {T}$ are the following:

${\displaystyle C_{1}=\{U^{0}=I\},}$

${\displaystyle C_{2}=\{U^{3}=-I\},}$

${\displaystyle C_{3}=\{\pm S,\pm V,\pm SV\},}$

${\displaystyle C_{4}=\{U^{2},SU^{2},VU^{2},SVU^{2}\},}$

${\displaystyle C_{5}=\{-U,SU,VU,SVU\},}$

${\displaystyle C_{6}=\{-U^{2},-SU^{2},-VU^{2},-SVU^{2}\},}$

${\displaystyle C_{7}=\{U,-SU,-VU,-SVU\}.}$

The character table of $\overline {T}$ is

Conjugacy Classes	$C_{1}$	$C_{2}$	$C_{3}$	$C_{4}$	$C_{5}$	$C_6$	${\displaystyle C_{7}}$
$\chi_1$	$1$	$1$	$1$	$1$	$1$	$1$	$1$
$\chi_2$	$1$	$1$	$1$	$\omega$	$\omega ^{2}$	$\omega$	$\omega ^{2}$
$\chi_3$	$1$	$1$	$1$	$\omega ^{2}$	$\omega$	$\omega ^{2}$	$\omega$
${\displaystyle \chi _{4}}$	$3$	$3$	$-1$	${\displaystyle 0}$	${\displaystyle 0}$	${\displaystyle 0}$	${\displaystyle 0}$
$c$	$2$	$-2$	${\displaystyle 0}$	$-1$	$-1$	$1$	$1$
${\displaystyle \chi _{5}}$	$2$	$-2$	${\displaystyle 0}$	$-\omega$	${\displaystyle -\omega ^{2}}$	$\omega$	$\omega ^{2}$
${\displaystyle \chi _{6}}$	$2$	$-2$	${\displaystyle 0}$	${\displaystyle -\omega ^{2}}$	$-\omega$	$\omega ^{2}$	$\omega$

Here ${\displaystyle \omega =e^{2\pi i/3}}$. The canonical representation is represented by c. By using the inner product, we have that the McKay graph of $\overline {T}$ is the extended Coxeter-Dynkin diagram of type ${\displaystyle {\tilde {E}}_{6}}$.

See also

• ADE classification
• Binary tetrahedral group

References

• Humphreys, James E. (1972), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0-387-90053-7
• James, Gordon; Liebeck, Martin (2001). Representations and Characters of Groups (2nd ed.). Cambridge University Press. ISBN 0-521-00392-X.
• Klein, Felix (1884), "Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünten Grade", Teubner, Leibniz
• McKay, John (1980), "Graphs, singularities and finite groups", Proc. Symp. Pure Math., Amer. Math. Soc., 37: 183–186, doi:10.1090/pspum/037/604577
• McKay, John (1982), "Representations and Coxeter Graphs", "The Geometric Vein", Coxeter Festschrift, Berlin: Springer-Verlag
• Riemenschneider, Oswald (2005), McKay correspondence for quotient surface singularities, Singularities in Geometry and Topology, Proceedings of the Trieste Singularity Summer School and Workshop, pp. 483–519
• Steinberg, Robert (1985), "Subgroups of ${\displaystyle SU_{2}}$, Dynkin diagrams and affine Coxeter elements", Pacific Journal of Mathematics, 18: 587–598